A Z-pontszám egy statisztikai érték, amely megmondja, hogy egy adott érték hány szórással rendelkezik a teljes adatkészlet átlagától. Az AVERAGE és STDEV.S vagy STDEV.P képletekkel kiszámíthatja az adatok átlagát és szórását, majd az eredmények alapján meghatározhatja az egyes értékek Z-pontszámát.
Tartalomjegyzék
Mi az a Z-pontszám, és mit csinálnak az AVERAGE, STDEV.S és STDEV.P függvények?
A Z-Score két különböző adatkészletből származó értékek összehasonlításának egyszerű módja. Úgy definiálható, hogy hány standard eltérés van az adatpont átlagától. Az általános képlet így néz ki:
=(DataPoint-AVERAGE(DataSet))/STDEV(DataSet)
Íme egy példa a tisztázáshoz. Tegyük fel, hogy össze akarta hasonlítani két algebrai diák teszteredményeit, amelyeket különböző tanárok tanítottak. Tudod, hogy az első tanuló 95%-ot ért el az egyik osztályban az érettségi vizsgán, a másik osztály tanulója pedig 87%-ot.
Első ránézésre impozánsabb a 95%-os osztályzat, de mi van, ha a második osztály tanára nehezebben vizsgázik? Kiszámolhatja az egyes tanulók pontszámának Z-pontszámát az egyes osztályok átlagpontszámai és az egyes osztályok pontszámainak szórása alapján. A két tanuló Z-pontszámát összevetve kiderülhet, hogy a 87%-os pontszámot elért tanuló jobban teljesített az osztály többi tagjához képest, mint a 98%-os pontszámmal rendelkező tanuló az osztály többi tagjához képest.
Az első statisztikai érték, amire szüksége van, az „átlag”, és az Excel „Átlag” függvénye kiszámítja ezt az értéket. Egyszerűen összeadja a cellatartomány összes értékét, és elosztja az összeget a számértékeket tartalmazó cellák számával (figyelmen kívül hagyja az üres cellákat).
A másik statisztikai érték, amire szükségünk van, a „szórás”, és az Excelnek két különböző funkciója van, amelyek kissé eltérő módon számítják ki a szórást.
Az Excel korábbi verzióiban csak az „STDEV” függvény volt, amely kiszámítja a szórást, miközben az adatokat egy sokaság „mintájaként” kezeli. Az Excel 2010 ezt két függvényre bontotta, amelyek a szórást számítják ki:
STDEV.S: Ez a funkció megegyezik az előző „STDEV” funkcióval. Kiszámítja a szórást, miközben az adatokat egy sokaság „mintájaként” kezeli. Egy populáció mintája lehet valami olyan, mint egy kutatási projekthez gyűjtött bizonyos szúnyogok vagy olyan autók, amelyeket félreállítottak és használtak az ütközésbiztonsági teszteléshez.
STDEV.P: Ez a függvény kiszámítja a szórást, miközben az adatokat a teljes sokaságként kezeli. Egy egész populáció olyan lenne, mint a Föld összes szúnyogja, vagy minden autó egy adott modell sorozatgyártásában.
Az, hogy melyiket választja, az adatkészletén alapul. A különbség általában kicsi, de az „STDEV.P” függvény eredménye mindig kisebb lesz, mint az „STDEV.S” függvény eredménye ugyanarra az adatkészletre. Konzervatívabb megközelítés azt feltételezni, hogy az adatok nagyobb változatosságot mutatnak.
Nézzünk egy példát
Példánkban két oszlop („Values” és „Z-Score”) és három „segítő” cellánk van az „ÁTLAG”, „STDEV.S” és „STDEV.P” függvények eredményeinek tárolására. Az „Értékek” oszlop tíz véletlen számot tartalmaz 500 körül, a „Z-Score” oszlopban pedig a „segítő” cellákban tárolt eredmények alapján számítjuk ki a Z-pontszámot.
Először is kiszámítjuk az értékek átlagát az „ÁTLAG” függvény segítségével. Válassza ki azt a cellát, ahol az „ÁTLAGOS” függvény eredményét tárolja.
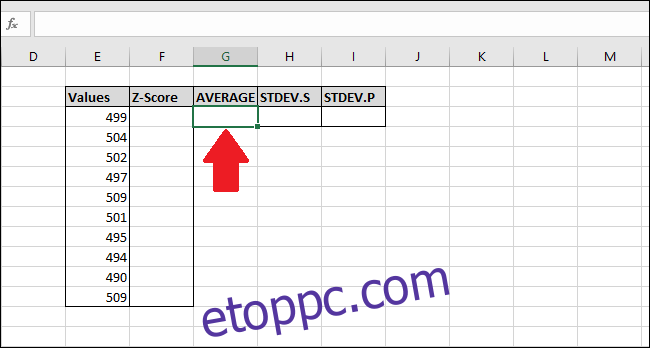
Írja be a következő képletet, és nyomja meg az enter billentyűt vagy használja a „Képletek” menüt.
=AVERAGE(E2:E13)
A funkció eléréséhez a „Képletek” menün keresztül válassza ki a „További függvények” legördülő listát, válassza a „Statisztika” lehetőséget, majd kattintson az „ÁTLAG” elemre.
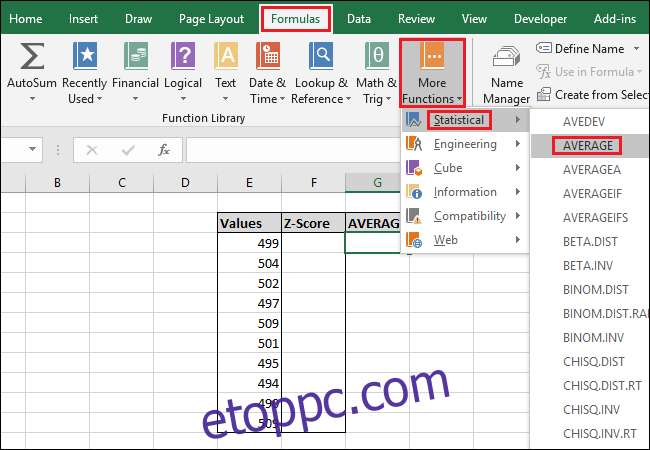
A Függvényargumentumok ablakban válassza ki az „Értékek” oszlop összes celláját a „Number1” mező bemeneteként. Nem kell aggódnia a „Szám2” mező miatt.
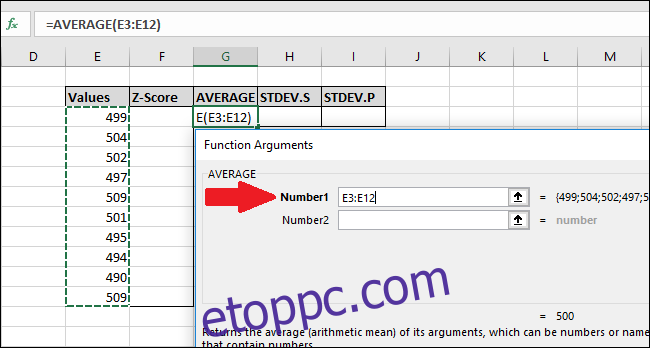
Most nyomja meg az „OK” gombot.
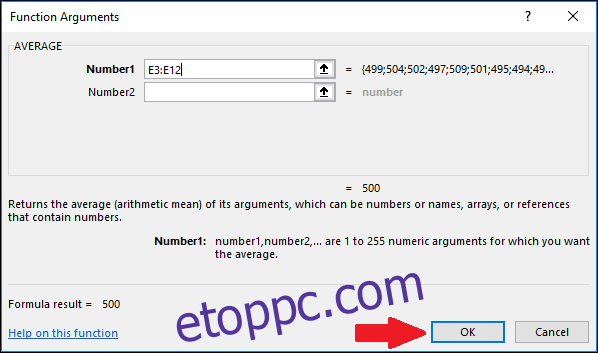
Ezután ki kell számítanunk az értékek szórását az „STDEV.S” vagy az „STDEV.P” függvény segítségével. Ebben a példában bemutatjuk, hogyan kell kiszámítani mindkét értéket, kezdve az „STDEV.S”-vel. Válassza ki azt a cellát, ahol az eredményt tárolni szeretné.
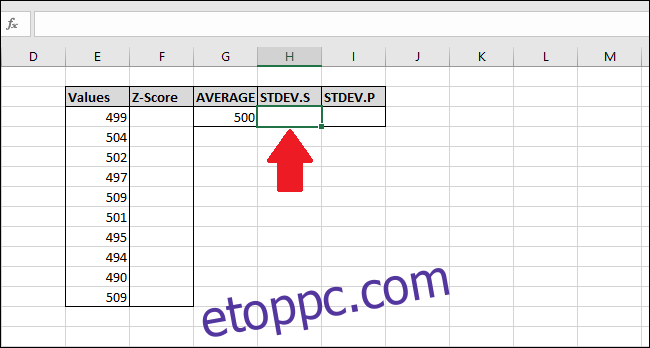
A szórás „STDEV.S” függvény segítségével történő kiszámításához írja be ezt a képletet, és nyomja meg az Enter billentyűt (vagy nyissa meg a „Képletek” menüből).
=STDEV.S(E3:E12)
A funkció eléréséhez a „Képletek” menün keresztül válassza ki a „További függvények” legördülő menüt, válassza a „Statistical” opciót, görgessen le egy kicsit, majd kattintson az „STDEV.S” parancsra.
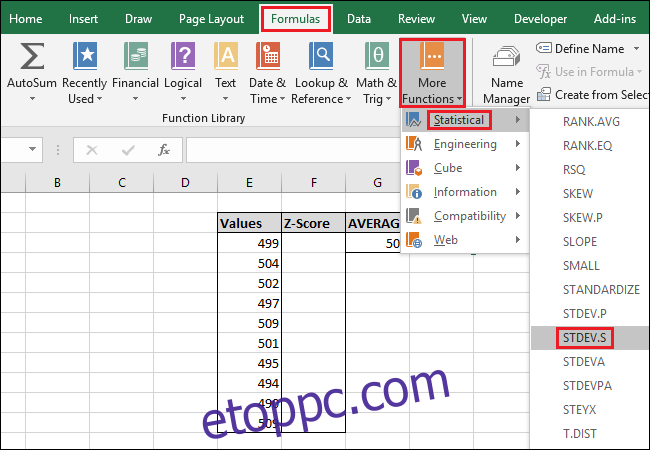
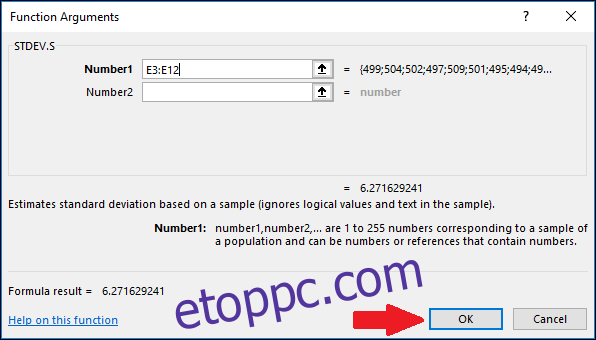
A Függvényargumentumok ablakban válassza ki az „Értékek” oszlop összes celláját a „Number1” mező bemeneteként. Itt sem kell aggódnia a „Szám2” mező miatt.
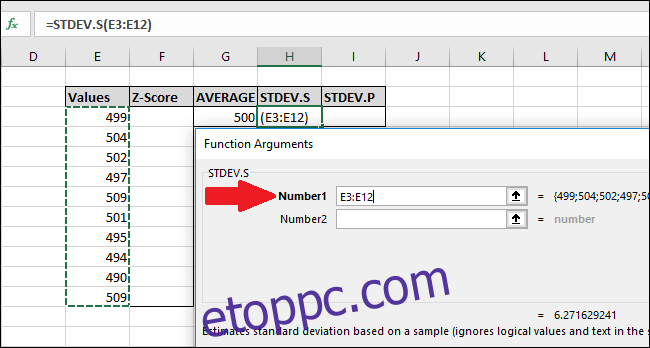
Most nyomja meg az „OK” gombot.
Ezután az „STDEV.P” függvény segítségével kiszámítjuk a szórást. Válassza ki azt a cellát, ahol az eredményt tárolni szeretné.
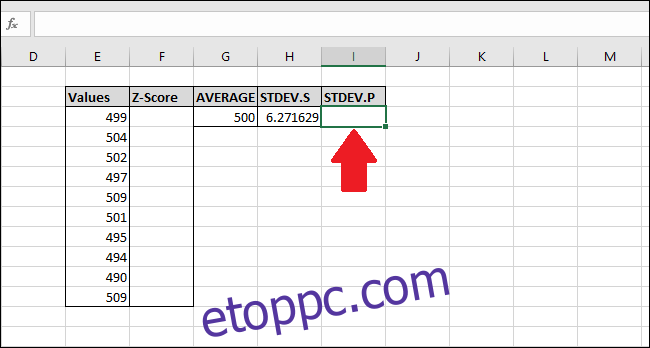
A szórás „STDEV.P” függvény segítségével történő kiszámításához írja be ezt a képletet, és nyomja meg az Enter billentyűt (vagy nyissa meg a „Képletek” menüből).
=STDEV.P(E3:E12)
A funkció eléréséhez a „Képletek” menün keresztül válassza ki a „További függvények” legördülő listát, válassza a „Statisztika” lehetőséget, görgessen le egy kicsit, majd kattintson az „STDEV.P” képletre.
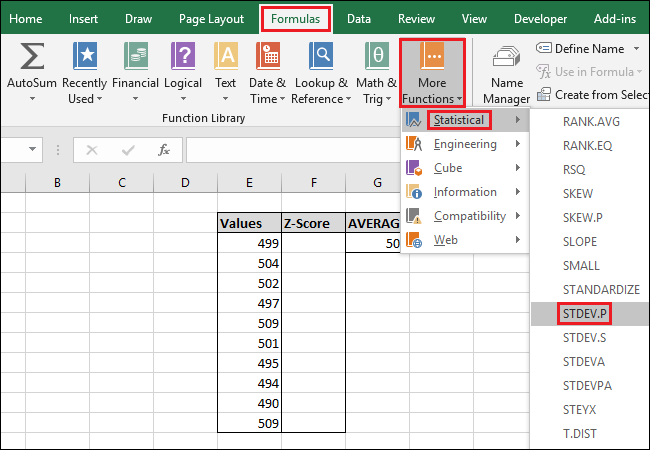
A Függvényargumentumok ablakban válassza ki az „Értékek” oszlop összes celláját a „Number1” mező bemeneteként. Ismét nem kell aggódnia a „Number2” mező miatt.
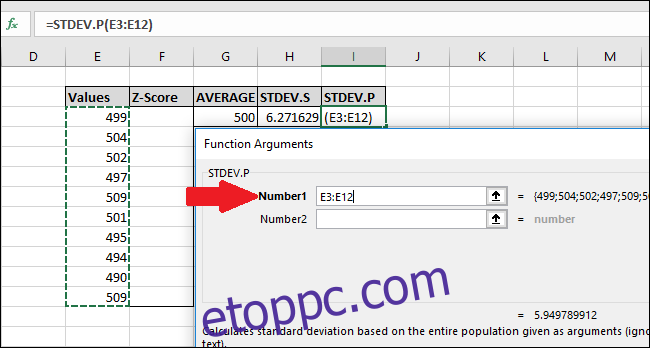
Most nyomja meg az „OK” gombot.
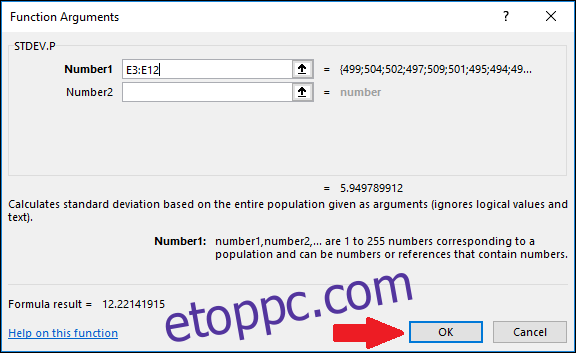
Most, hogy kiszámítottuk adataink átlagát és szórását, minden megvan, ami a Z-pontszám kiszámításához szükséges. Használhatunk egy egyszerű képletet, amely hivatkozik az „AVERAGE” és „STDEV.S” vagy „STDEV.P” függvények eredményeit tartalmazó cellákra.
Válassza ki az első cellát a „Z-Score” oszlopban. Ebben a példában az „STDEV.S” függvény eredményét fogjuk használni, de használhatjuk az „STDEV.P” függvény eredményét is.
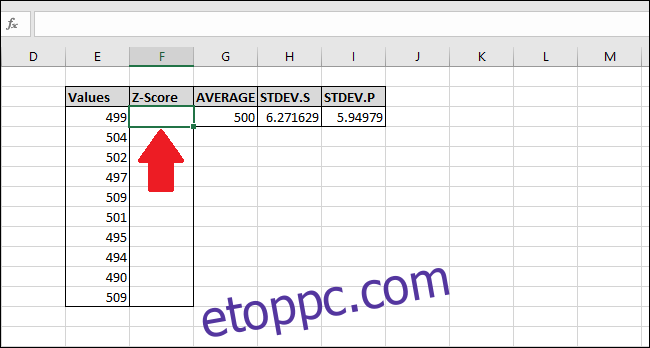
Írja be a következő képletet, és nyomja meg az Enter billentyűt:
=(E3-$G$3)/$H$3
Alternatív megoldásként a következő lépésekkel is beírhatja a képletet gépelés helyett:
Kattintson az F3 cellára, és írja be: =(
Válassza ki az E3 cellát. (Egyszer megnyomhatja a bal nyílbillentyűt, vagy használhatja az egeret)
Írja be a mínusz jelet –
Jelölje ki a G3 cellát, majd nyomja meg az F4 billentyűt a „$” karakterek hozzáadásához, hogy „abszolút” hivatkozást képezzen a cellára (a „G3” > „$G$3″ > „G$3” > „$G3” > „G3” ” ha tovább nyomod az F4 billentyűt)
Típus )/
Válassza ki a H3 cellát (vagy az I3 cellát, ha „STDEV.P”-t használ), és nyomja meg az F4 billentyűt a két „$” karakter hozzáadásához.
nyomd meg az Entert
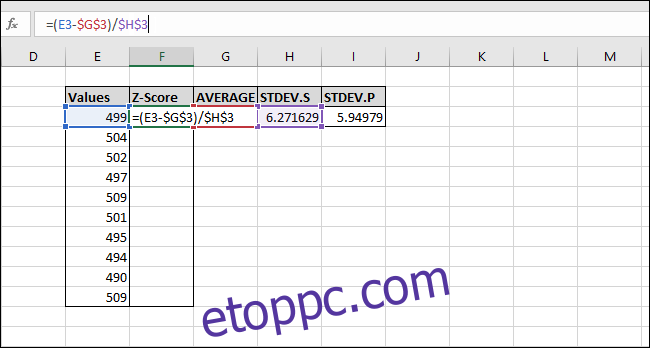
A Z-pontszám az első értékre lett kiszámítva. 0,15945 szórással az átlag alatt van. Az eredmények ellenőrzéséhez megszorozhatja a szórást ezzel az eredménnyel (6,271629 * -0,15945), és ellenőrizheti, hogy az eredmény egyenlő-e az érték és az átlag különbségével (499-500). Mindkét eredmény egyenlő, így az értéknek van értelme.
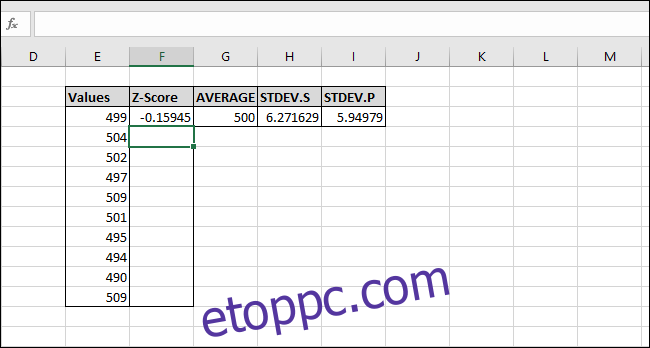
Számítsuk ki a többi érték Z-pontszámát. Jelölje ki a teljes „Z-Score” oszlopot a képletet tartalmazó cellával kezdve.
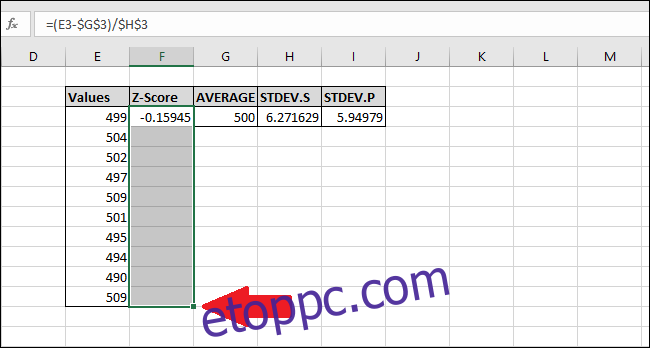
Nyomja meg a Ctrl+D billentyűkombinációt, amely lemásolja a felső cellában lévő képletet az összes többi kijelölt cellába.
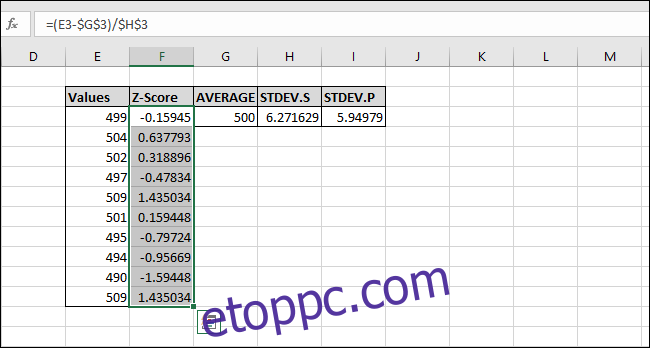
Mostanra a képletet az összes cellára „feltöltötték”, és mindegyik mindig a megfelelő „AVERAGE” és „STDEV.S” vagy „STDEV.P” cellákra hivatkozik a „$” karakterek miatt. Ha hibákat kap, lépjen vissza, és ellenőrizze, hogy a „$” karakterek szerepelnek-e a megadott képletben.
A Z-pontszám kiszámítása „Helper” cellák használata nélkül
A segítő cellák tárolják az eredményeket, például az „ÁTLAG”, „STDEV.S” és „STDEV.P” függvények eredményeit. Hasznosak lehetnek, de nem mindig szükségesek. Ezeket teljesen kihagyhatja a Z-pontszám kiszámításakor a következő általános képletekkel.
Íme, az „STDEV.S” függvényt használó:
=(Value-AVERAGE(Values))/STDEV.S(Values)
És egy a „STEV.P” funkcióval:
=(Value-AVERAGE(Values))/STDEV.P(Values)
Amikor megadja a függvényekben az „Értékek” cellatartományát, feltétlenül adjon hozzá abszolút hivatkozásokat („$” az F4 billentyűvel), hogy „kitöltéskor” ne egy másik tartomány átlagát vagy szórását számítsa ki. minden képletben.
Ha nagy adatkészlettel rendelkezik, akkor hatékonyabb lehet a segédcellák használata, mert nem minden alkalommal számítja ki az „ÁTLAG” és „STDEV.S” vagy „STDEV.P” függvények eredményét, ezzel megtakarítva a processzor erőforrásait és felgyorsítja az eredmények kiszámításához szükséges időt.
Ezenkívül a „$G$3” kevesebb bájtot igényel a tároláshoz és kevesebb RAM-ot a betöltéshez, mint az „ÁTLAGOS($3:$E$12).”. Ez azért fontos, mert az Excel szabványos 32 bites verziója 2 GB RAM-ra korlátozódik (a 64 bites verzióban nincs korlátozás arra vonatkozóan, hogy mennyi RAM használható).