Lineare Kalibrierungskurven in Excel erstellen und nutzen
Excel bietet praktische Funktionen, um Kalibrierungsdaten zu visualisieren und eine optimale Ausgleichsgerade zu berechnen. Dies ist besonders nützlich beim Erstellen von Berichten im Chemielabor oder bei der Programmierung von Korrekturfaktoren in Geräten.
In diesem Artikel zeigen wir, wie man in Excel ein Diagramm für eine lineare Kalibrierungskurve erstellt, die Formel der Kurve anzeigt und mit den Funktionen STEIGUNG und ACHSENABSCHNITT einfache Formeln aufstellt, um die Kalibrierungsgleichung in Excel anzuwenden.
Was ist eine Kalibrierungskurve und wie unterstützt Excel dabei?
Bei einer Kalibrierung werden die Messwerte eines Geräts (z.B. die Temperaturanzeige eines Thermometers) mit bekannten Werten, sogenannten Standards, verglichen (z.B. Gefrier- und Siedepunkt von Wasser). Dadurch entsteht eine Reihe von Datenpaaren, aus denen eine Kalibrierungskurve entwickelt wird.
Eine Zwei-Punkt-Kalibrierung eines Thermometers unter Verwendung des Gefrier- und Siedepunkts von Wasser ergibt zwei Datenpaare: eins beim Eintauchen in Eiswasser (0 °C) und eins in kochendes Wasser (100 °C). Diese Datenpaare werden als Punkte in einem Diagramm dargestellt, und eine Linie (die Kalibrierungskurve) wird zwischen ihnen gezogen. Unter der Annahme einer linearen Beziehung kann jeder Punkt auf dieser Linie dazu verwendet werden, von einem abgelesenen Wert des Thermometers auf die entsprechende „wahre“ Temperatur zu schließen.
Die Linie füllt somit die Lücke zwischen den bekannten Werten. So können Sie beispielsweise eine fundierte Schätzung der tatsächlichen Temperatur bei einer Anzeige von 57,2 Grad auf dem Thermometer vornehmen, auch wenn Sie diesen Wert noch nicht mit einem Standard verglichen haben.
Excel ermöglicht die grafische Darstellung von Datenpaaren, das Hinzufügen einer Trendlinie (Kalibrierungskurve) und das Anzeigen der zugehörigen Gleichung. Neben der visuellen Darstellung kann die Formel der Linie auch mit den Funktionen STEIGUNG und ACHSENABSCHNITT von Excel berechnet werden. Diese Werte können dann in Formeln eingebunden werden, um für jede Messung automatisch den „wahren“ Wert zu bestimmen.
Ein praktisches Beispiel
In unserem Beispiel entwickeln wir eine Kalibrierungskurve aus zehn Datenpaaren mit jeweils einem X- und einem Y-Wert. Die X-Werte repräsentieren unsere „Standards“ und können beispielsweise die Konzentration einer chemischen Lösung oder die Eingabevariable eines Programms zur Steuerung einer Ballwurfmaschine sein.
Die Y-Werte sind die zugehörigen Messwerte und repräsentieren beispielsweise die Messergebnisse des Messinstruments bei jeder chemischen Lösung oder die mit jedem Eingabewert gemessene Flugweite des Balls.
Nachdem wir die Kalibrierungskurve grafisch dargestellt haben, nutzen wir die Funktionen STEIGUNG und ACHSENABSCHNITT, um die Formel der Kalibrierungsgeraden zu berechnen und daraus die Konzentration einer unbekannten chemischen Lösung zu ermitteln oder die passenden Eingaben für die Ballwurfmaschine zu finden.
Schritt 1: Erstellen des Diagramms
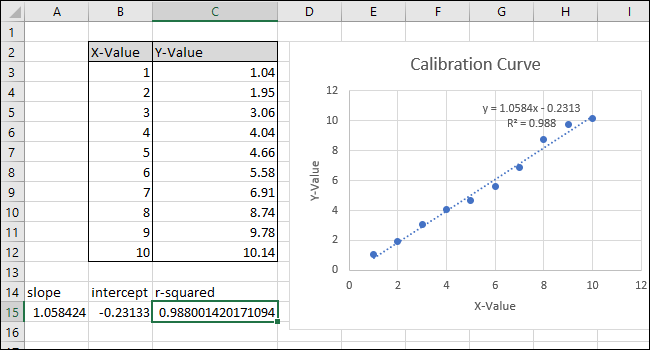
Unsere Beispieltabelle besteht aus zwei Spalten: „X-Wert“ und „Y-Wert“.
Beginnen Sie mit der Auswahl der Daten, die im Diagramm dargestellt werden sollen.
Wählen Sie zuerst die Zellen in der Spalte „X-Wert“ aus.

Halten Sie nun die Strg-Taste gedrückt und klicken Sie auf die Zellen der Spalte „Y-Wert“.

Gehen Sie zur Registerkarte „Einfügen“.

Navigieren Sie zum Menü „Diagramme“ und wählen Sie die erste Option im Dropdown-Menü „Punkt(XY)“.
Es wird ein Diagramm mit den Datenpunkten beider Spalten angezeigt.
Wählen Sie die Datenreihe aus, indem Sie auf einen der blauen Punkte klicken. Nach der Auswahl werden die Punkte in Excel hervorgehoben.

Klicken Sie mit der rechten Maustaste auf einen der Punkte und wählen Sie dann die Option „Trendlinie hinzufügen“.

Eine gerade Linie wird im Diagramm angezeigt.

Auf der rechten Seite des Bildschirms erscheint das Menü „Trendlinie formatieren“. Aktivieren Sie die Kontrollkästchen neben „Gleichung im Diagramm anzeigen“ und „R-Quadrat-Wert im Diagramm anzeigen“. Der R-Quadrat-Wert gibt an, wie gut die Linie zu den Daten passt. Der optimale R-Quadrat-Wert ist 1,000, bei dem jeder Datenpunkt auf der Linie liegt. Bei wachsenden Abweichungen sinkt der R-Quadrat-Wert, mit 0,000 als niedrigstem Wert.

Die Gleichung und die R-Quadrat-Statistik der Trendlinie werden nun im Diagramm angezeigt. In unserem Beispiel ist die Datenkorrelation mit einem R-Quadrat-Wert von 0,988 sehr gut.
Die Gleichung hat die Form „Y = Mx + B“, wobei M die Steigung und B der y-Achsenabschnitt ist.

Nachdem die Kalibrierung nun abgeschlossen ist, können wir das Diagramm anpassen, indem wir den Titel bearbeiten und Achsentitel hinzufügen.
Um den Diagrammtitel zu ändern, klicken Sie darauf, um den Text auszuwählen.

Geben Sie nun einen neuen Titel ein, der das Diagramm beschreibt.

Um Titel zur X- und Y-Achse hinzuzufügen, navigieren Sie zuerst zu „Diagrammtools > Design“.

Klicken Sie auf das Dropdown-Menü „Diagrammelement hinzufügen“.
Wählen Sie dann „Achsentitel > Primäre Horizontale“.

Ein Achsentitel wird angezeigt.
Um den Achsentitel umzubenennen, wählen Sie zuerst den Text aus und geben dann einen neuen Titel ein.

Gehen Sie nun zu „Achsentitel > Primäre Vertikale“.

Ein Achsentitel wird angezeigt.

Benennen Sie diesen Titel um, indem Sie den Text auswählen und einen neuen Titel eingeben.

Ihr Diagramm ist jetzt fertig.

Schritt 2: Berechnung der Liniengleichung und R-Quadrat-Statistik
Nun berechnen wir die Liniengleichung und die R-Quadrat-Statistik mit den Excel-Funktionen STEIGUNG, ACHSENABSCHNITT und KORREL.
In unserem Blatt (Zeile 14) haben wir Überschriften für diese drei Funktionen hinzugefügt. Die tatsächlichen Berechnungen führen wir in den Zellen unterhalb dieser Überschriften durch.
Zuerst berechnen wir die STEIGUNG. Wählen Sie Zelle A15 aus.

Navigieren Sie zu „Formeln > Weitere Funktionen > Statistik > STEIGUNG“.

Das Fenster für die Funktionsargumente wird angezeigt. Wählen oder geben Sie im Feld „Bekannte_y“ die Zellen der Spalte „Y-Wert“ ein.
Wählen oder geben Sie im Feld „Bekannte_x“ die Zellen der Spalte „X-Wert“ ein. Die Reihenfolge von „Bekannte_y“ und „Bekannte_x“ ist in der Funktion STEIGUNG wichtig.

Klicken Sie auf „OK“. Die finale Formel in der Bearbeitungsleiste sollte wie folgt aussehen:
=STEIGUNG(C3:C12;B3:B12)
Beachten Sie, dass der von der Funktion STEIGUNG in Zelle A15 zurückgegebene Wert mit dem im Diagramm angezeigten Wert übereinstimmt.

Wählen Sie als Nächstes Zelle B15 aus und navigieren Sie zu „Formeln > Weitere Funktionen > Statistik > ACHSENABSCHNITT“.

Das Fenster für die Funktionsargumente wird angezeigt. Wählen oder geben Sie im Feld „Bekannte_y“ die Zellen der Spalte „Y-Wert“ ein.
Wählen oder geben Sie im Feld „Bekannte_x“ die Zellen der Spalte „X-Wert“ ein. Die Reihenfolge von „Bekannte_y“ und „Bekannte_x“ ist auch bei der Funktion ACHSENABSCHNITT wichtig.

Klicken Sie auf „OK“. Die finale Formel in der Bearbeitungsleiste sollte wie folgt aussehen:
=ACHSENABSCHNITT(C3:C12;B3:B12)
Beachten Sie, dass der von der Funktion ACHSENABSCHNITT zurückgegebene Wert dem im Diagramm angezeigten y-Achsenabschnitt entspricht.

Wählen Sie als Nächstes Zelle C15 aus und navigieren Sie zu „Formeln > Weitere Funktionen > Statistik > KORREL“.

Das Fenster für die Funktionsargumente wird angezeigt. Wählen oder geben Sie einen der beiden Zellbereiche für das Feld „Matrix1“ ein. Im Gegensatz zu STEIGUNG und ACHSENABSCHNITT spielt die Reihenfolge für die Funktion KORREL keine Rolle.
Wählen oder geben Sie den anderen der beiden Zellbereiche für das Feld „Matrix2“ ein.

Klicken Sie auf „OK“. Die Formel in der Bearbeitungsleiste sollte nun so aussehen:
=KORREL(B3:B12;C3:C12)
Beachten Sie, dass der von der Funktion KORREL zurückgegebene Wert nicht mit dem R-Quadrat-Wert im Diagramm übereinstimmt. Die Funktion KORREL gibt „R“ zurück, daher müssen wir das Ergebnis quadrieren, um „R-Quadrat“ zu berechnen.

Klicken Sie in die Bearbeitungsleiste und fügen Sie am Ende der Formel „^2“ hinzu, um den von der Funktion KORREL zurückgegebenen Wert zu quadrieren. Die fertige Formel sollte nun so aussehen:
=KORREL(B3:B12;C3:C12)^2
Drücken Sie die Eingabetaste.

Nach der Änderung der Formel stimmt der R-Quadrat-Wert nun mit dem im Diagramm angezeigten Wert überein.
Schritt 3: Formeln zur schnellen Berechnung von Werten erstellen
Mit diesen Werten können wir nun einfache Formeln verwenden, um die Konzentration einer unbekannten Lösung oder die Eingabe für die Ballwurfmaschine zu bestimmen.
In diesen Schritten werden die Formeln erstellt, mit denen Sie einen X- oder Y-Wert eingeben und den entsprechenden Wert auf Basis der Kalibrierungskurve erhalten.

Die Formel der Ausgleichsgeraden lautet „Y-Wert = STEIGUNG * X-Wert + ACHSENABSCHNITT“. Um nach dem „Y-Wert“ aufzulösen, multiplizieren Sie den X-Wert mit der STEIGUNG und addieren dann den ACHSENABSCHNITT.

Als Beispiel geben wir Null als X-Wert ein. Der zurückgegebene Y-Wert sollte dem ACHSENABSCHNITT der Ausgleichsgeraden entsprechen. Da dies der Fall ist, wissen wir, dass die Formel korrekt funktioniert.

Das Auflösen nach dem X-Wert auf Basis eines Y-Wertes erfolgt durch Subtrahieren des ACHSENABSCHNITTS vom Y-Wert und Teilen des Ergebnisses durch die STEIGUNG:
X-Wert = (Y-Wert - ACHSENABSCHNITT) / STEIGUNG

Als Beispiel haben wir den ACHSENABSCHNITT als Y-Wert verwendet. Der zurückgegebene X-Wert sollte Null sein, ist aber 3,14934E-06. Der zurückgegebene Wert ist nicht exakt Null, da wir das Ergebnis des ACHSENABSCHNITTS bei der Eingabe versehentlich abgeschnitten haben. Die Formel funktioniert jedoch korrekt, da das Ergebnis der Formel 0,00000314934 ist, was im Wesentlichen Null ist.

Sie können nun einen beliebigen X-Wert in die erste Zelle mit dem fetten Rahmen eingeben, und Excel berechnet automatisch den entsprechenden Y-Wert.

Wenn Sie einen beliebigen Y-Wert in die zweite Zelle mit dem fetten Rahmen eingeben, erhalten Sie den entsprechenden X-Wert. Diese Formel verwenden Sie, um die Konzentration einer Lösung zu berechnen oder die benötigte Eingabe zu ermitteln, damit die Kugel eine bestimmte Entfernung zurücklegt.

In diesem Fall zeigt das Messinstrument „5“ an. Die Kalibrierung würde daher eine Konzentration von 4,94 vorschlagen. Oder, wenn wir möchten, dass die Kugel eine Distanz von fünf Einheiten zurücklegt, sollten wir 4,94 als Eingabevariable für das Programm verwenden, das den Ballwerfer steuert. Aufgrund des hohen R-Quadrat-Wertes in diesem Beispiel können wir den Ergebnissen ein hohes Vertrauen schenken.