Die Support Vector Machine, oft abgekürzt als SVM, gehört zu den bekanntesten und vielseitigsten Algorithmen im Bereich des maschinellen Lernens. Sie zeichnet sich durch ihre Effizienz und ihre Fähigkeit aus, auch mit begrenzten Datenmengen präzise Modelle zu erstellen. Doch was genau verbirgt sich hinter dieser Bezeichnung?
Was ist eine Support Vector Machine (SVM)?
Eine Support Vector Machine ist ein Algorithmus für maschinelles Lernen, der auf überwachtem Lernen basiert und dazu dient, Modelle für die binäre Klassifizierung zu entwickeln. Diese Definition mag zunächst komplex erscheinen. Daher wird dieser Artikel die Funktionsweise von SVM und ihre Rolle in der Verarbeitung natürlicher Sprache näher erläutern. Zunächst wollen wir aber die grundlegende Arbeitsweise einer Support Vector Machine beleuchten.
Wie funktioniert SVM?
Betrachten wir ein vereinfachtes Klassifizierungsproblem: Wir haben Datenpunkte, die sich durch zwei Merkmale, x und y, auszeichnen, und eine zugehörige Klassifizierung, die entweder rot oder blau ist. Eine grafische Darstellung dieser Daten könnte folgendermaßen aussehen:
Die Aufgabe besteht nun darin, eine Entscheidungsgrenze zu finden, die die beiden Klassen trennt. Eine Entscheidungsgrenze ist im Wesentlichen eine Linie, die diese Trennung visuell darstellt. Hier sehen wir denselben Datensatz, diesmal mit einer eingezeichneten Entscheidungsgrenze:
Mit dieser Entscheidungsgrenze können wir nun Vorhersagen treffen: Je nachdem, auf welcher Seite der Grenze ein Datenpunkt liegt, können wir ihn einer bestimmten Klasse zuordnen. Der Algorithmus der Support Vector Machine zielt darauf ab, die optimalste Entscheidungsgrenze zu definieren, die für diese Klassifizierung verwendet werden kann.
Aber was genau bedeutet „optimale Entscheidungsgrenze“?
Man könnte argumentieren, dass die beste Entscheidungsgrenze jene ist, die den maximalen Abstand zu den sogenannten Support-Vektoren hat. Support-Vektoren sind jene Datenpunkte jeder Klasse, die der jeweils anderen Klasse am nächsten sind. Diese Punkte sind besonders relevant, da sie aufgrund ihrer Nähe zur anderen Klasse das größte Risiko einer Fehlklassifizierung bergen.
Das Training einer Support Vector Machine beinhaltet also die Suche nach einer Linie, die den Spielraum zwischen diesen Support-Vektoren maximiert.
Wichtig ist auch zu wissen, dass die Position der Entscheidungsgrenze ausschließlich durch die Support-Vektoren bestimmt wird. Alle anderen Datenpunkte sind im Grunde genommen irrelevant für die Bestimmung dieser Grenze. Daher sind für das Training lediglich die Support-Vektoren notwendig.
In diesem Beispiel wird die Entscheidungsgrenze als gerade Linie dargestellt. Das liegt daran, dass unser Datensatz nur zwei Merkmale besitzt. Wenn ein Datensatz drei Merkmale aufweist, wäre die Entscheidungsgrenze eine Ebene. Bei vier oder mehr Merkmalen spricht man von einer Hyperebene.
Nicht linear trennbare Daten
Das bisherige Beispiel basierte auf einfachen Daten, die sich mit einer linearen Entscheidungsgrenze trennen ließen. Betrachten wir nun einen Fall, in dem die Daten wie folgt angeordnet sind:
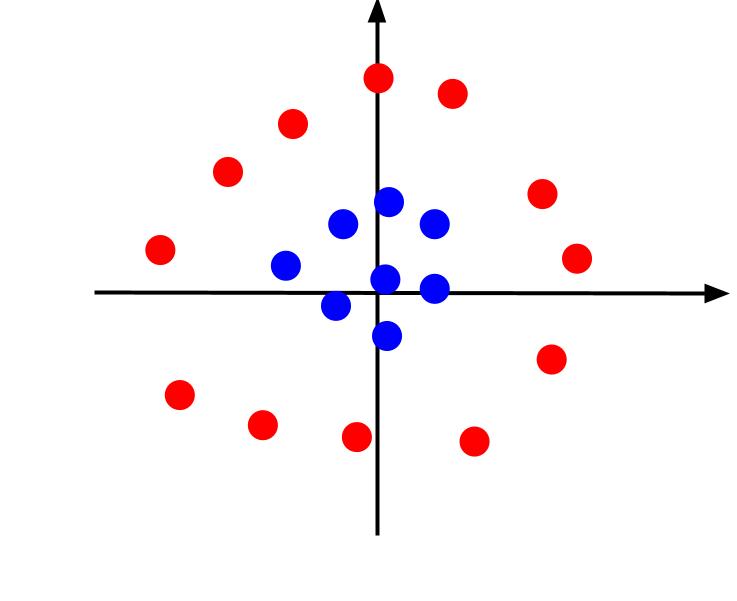
In diesem Szenario ist es unmöglich, die Daten durch eine einfache Linie zu trennen. Allerdings können wir ein zusätzliches Merkmal z definieren, zum Beispiel über die Formel z = x^2 + y^2. Dies erlaubt uns, die Daten als dreidimensionales Diagramm darzustellen, indem wir z als dritte Achse hinzufügen.
Wenn wir das 3D-Diagramm so betrachten, dass die x-Achse horizontal und die z-Achse vertikal verläuft, erhalten wir diese Perspektive:
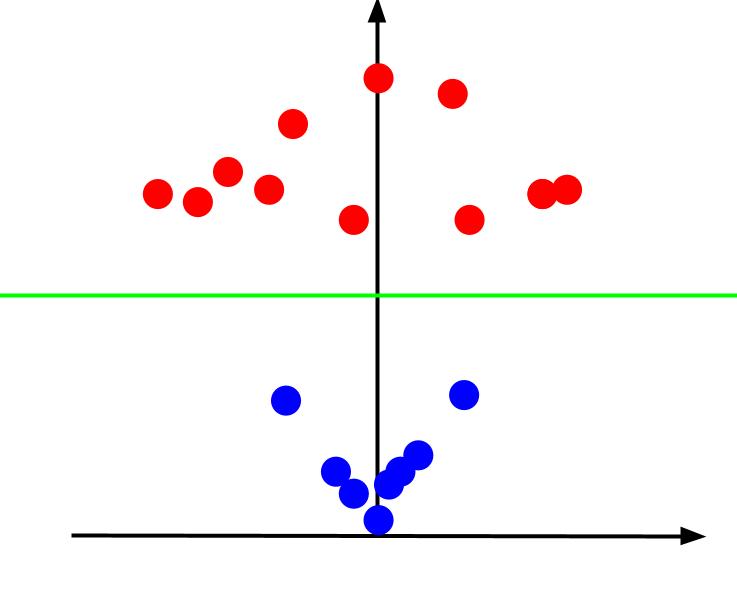
Der z-Wert gibt an, wie weit ein Punkt in der alten XY-Ebene vom Ursprung entfernt ist. Die blauen Punkte, die näher am Ursprung liegen, haben niedrigere z-Werte. Die roten Punkte, die weiter vom Ursprung entfernt sind, haben höhere z-Werte. Durch die Auftragung gegen die z-Werte erhalten wir eine klare Klassifizierung, die durch eine lineare Entscheidungsgrenze abgetrennt werden kann.
Dies ist eine zentrale Idee bei Support Vector Machines. Allgemeiner formuliert: Wir erweitern die Dimensionen, bis die Datenpunkte durch eine lineare Grenze trennbar werden. Die dafür zuständigen Funktionen werden als Kernel-Funktionen bezeichnet. Es gibt verschiedene Kernel-Funktionen wie Sigmoid, Linear, Non-Linear und RBF.
Um die Zuordnung dieser Funktionen effizienter zu gestalten, verwendet SVM einen Kernel-Trick.
SVM im maschinellen Lernen
Die Support Vector Machine ist, neben Algorithmen wie Entscheidungsbäumen und neuronalen Netzen, ein wichtiger Bestandteil des Werkzeugkastens im Bereich des maschinellen Lernens. Ihre Beliebtheit rührt daher, dass sie auch mit geringeren Datenmengen gute Ergebnisse erzielt. SVMs werden häufig verwendet für:
- Textklassifizierung: Einordnung von Textdaten wie Kommentaren und Rezensionen in vordefinierte Kategorien.
- Gesichtserkennung: Analyse von Bildern, um Gesichter zu identifizieren, zum Beispiel für Augmented-Reality-Filter.
- Bildklassifizierung: Effiziente Einordnung von Bildern im Vergleich zu anderen Methoden.
Das Textklassifikationsproblem
Das Internet ist eine schier unendliche Quelle von Textdaten. Viele dieser Daten sind jedoch unstrukturiert und nicht klassifiziert. Um diese Daten besser nutzen und verstehen zu können, ist eine Klassifizierung unerlässlich. Beispiele hierfür sind:
- Die Kategorisierung von Tweets nach Themen, um Nutzern das Folgen relevanter Informationen zu erleichtern.
- Die Sortierung von E-Mails in Kategorien wie „Soziale Netzwerke“, „Werbung“ oder „Spam“.
- Die Klassifizierung von Kommentaren in öffentlichen Foren als „hasserfüllt“ oder „obszön“.
Funktionsweise von SVM mit Natural Language Classification
Support Vector Machines können verwendet werden, um Texte danach zu klassifizieren, ob sie einem bestimmten Thema zugehörig sind oder nicht. Dafür werden die Textdaten in einen Datensatz mit mehreren Merkmalen umgewandelt.
Eine Methode hierfür ist, für jedes einzelne Wort im Datensatz ein eigenes Merkmal zu erstellen. Dann wird für jeden Textdatenpunkt festgehalten, wie oft jedes Wort vorkommt. Wenn der Datensatz beispielsweise aus eindeutigen Wörtern besteht, haben wir im Datensatz entsprechend viele Merkmale.
Zusätzlich werden Klassifizierungen für diese Datenpunkte angegeben. Obwohl diese Klassifizierungen in der Regel durch Text beschrieben werden, erwarten die meisten SVM-Implementierungen numerische Beschriftungen. Daher müssen Sie diese Beschriftungen vor dem Training in Zahlen umwandeln. Nachdem der Datensatz vorbereitet und diese Merkmale als Koordinaten verwendet wurden, kann der Text mit einem SVM-Modell klassifiziert werden.
Erstellen einer SVM in Python
Um eine Support Vector Machine (SVM) in Python zu erstellen, kann man die SVC-Klasse aus der sklearn.svm-Bibliothek verwenden. Hier ist ein Beispiel, wie die SVC-Klasse verwendet werden kann, um ein SVM-Modell in Python zu erstellen:
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
# Lade den Datensatz
X = ...
y = ...
# Teile die Daten in Trainings- und Testsets auf
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=19)
# Erstelle ein SVM-Modell
model = SVC(kernel="linear")
# Trainiere das Modell mit den Trainingsdaten
model.fit(X_train, y_train)
# Evaluiere das Modell mit den Testdaten
accuracy = model.score(X_test, y_test)
print("Accuracy: ", accuracy)
In diesem Beispiel importieren wir zuerst die SVC-Klasse aus der sklearn.svm-Bibliothek. Dann laden wir den Datensatz und teilen ihn in Trainings- und Testsets auf.
Als Nächstes erstellen wir ein SVM-Modell, indem wir ein SVC-Objekt instanziieren und den Kernel-Parameter als „linear“ angeben. Anschließend trainieren wir das Modell mit den Trainingsdaten mithilfe der Fit-Methode und evaluieren es mit den Testdaten und der Score-Methode. Die Score-Methode gibt die Genauigkeit des Modells zurück, die wir auf der Konsole ausgeben.
Es können auch andere Parameter für das SVC-Objekt angegeben werden, z. B. der C-Parameter, der die Stärke der Regularisierung steuert, und der Gamma-Parameter, der den Kernel-Koeffizienten für bestimmte Kernel steuert.
Vorteile von SVM
Hier ist eine Liste von Vorteilen der Verwendung von Support Vector Machines (SVMs):
- Effizienz: SVMs sind im Allgemeinen effizient im Training, besonders bei großen Stichproben.
- Robustheit gegenüber Rauschen: SVMs sind relativ robust gegenüber Rauschen in den Trainingsdaten, da sie versuchen, einen Klassifikator mit maximalem Spielraum zu finden. Das macht sie weniger anfällig für Störungen als andere Methoden.
- Speichereffizienz: SVMs benötigen nur eine Teilmenge der Trainingsdaten im Speicher, was sie speichereffizienter als andere Algorithmen macht.
- Effektiv in hochdimensionalen Räumen: SVMs können auch bei einer höheren Anzahl von Merkmalen als Stichproben gut funktionieren.
- Vielseitigkeit: SVMs sind sowohl für Klassifizierungs- als auch für Regressionsaufgaben einsetzbar und können unterschiedliche Datentypen, einschließlich linearer und nichtlinearer Daten, verarbeiten.
Lassen Sie uns nun einige der besten Ressourcen zum Erlernen der Support Vector Machine (SVM) ansehen.
Lernmittel
Eine Einführung in Support Vector Machines
Dieses Buch bietet eine umfassende und schrittweise Einführung in Kernel-basierte Lernmethoden.
Es vermittelt Ihnen ein fundiertes Verständnis der Theorie hinter den Support Vector Machines.
Anwendungen von Support Vector Machines
Während sich das erste Buch auf die Theorie konzentrierte, widmet sich dieses Buch den praktischen Anwendungen von Support Vector Machines.
Es untersucht, wie SVMs in der Bildverarbeitung, Mustererkennung und Computer Vision eingesetzt werden.
Support Vector Machines (Informationswissenschaft und Statistik)
Dieses Buch bietet einen Überblick über die Prinzipien, die der Effektivität von Support Vector Machines (SVMs) in verschiedenen Anwendungen zugrunde liegen.
Die Autoren beleuchten mehrere Faktoren, die zum Erfolg von SVMs beitragen. Dazu gehören die Fähigkeit, mit wenigen Parametern eine gute Leistung zu erzielen, die Widerstandsfähigkeit gegenüber Fehlern und Anomalien sowie eine effiziente Rechenleistung im Vergleich zu anderen Methoden.
Lernen mit Kerneln
„Learning with Kernels“ ist ein Buch, das die Leser in die Welt der Support Vector Machines (SVMs) und verwandter Kernel-Techniken einführt.
Es ist so aufgebaut, dass Leser ein grundlegendes Verständnis der Mathematik und des Wissens erlangen, das sie für den Einsatz von Kernel-Algorithmen beim maschinellen Lernen benötigen. Das Buch zielt darauf ab, eine gründliche und dennoch zugängliche Einführung in SVMs und Kernel-Methoden zu bieten.
Support Vector Machines mit Sci-kit Learn
Dieser Online-Kurs „Support Vector Machines with Sci-kit Learn“ des Coursera-Projektnetzwerks vermittelt, wie ein SVM-Modell mithilfe der beliebten Bibliothek für maschinelles Lernen, Sci-Kit Learn, implementiert wird.

Darüber hinaus lernen Sie die Theorie hinter SVMs kennen und ermitteln ihre Stärken und Grenzen. Der Kurs ist für Anfänger geeignet und dauert etwa 2,5 Stunden.
Support Vector Machines in Python: Konzepte und Code
Dieser kostenpflichtige Online-Kurs zu Support Vector Machines in Python von Udemy bietet bis zu 6 Stunden videobasierte Anleitung und wird mit einem Zertifikat abgeschlossen.

Der Kurs behandelt SVMs und ihre Implementierung mit Python. Außerdem werden Geschäftsanwendungen von Support Vector Machines behandelt.
Maschinelles Lernen und KI: Support Vector Machines in Python
In diesem Kurs zu maschinellem Lernen und KI erfahren Sie, wie Sie Support Vector Machines (SVMs) für verschiedene praktische Anwendungen verwenden, darunter Bilderkennung, Spam-Erkennung, medizinische Diagnose und Regressionsanalyse.

Sie verwenden die Programmiersprache Python, um ML-Modelle für diese Anwendungen zu implementieren.
Letzte Worte
In diesem Artikel haben wir uns grundlegend mit der Theorie der Support Vector Machines befasst und ihre Anwendungen im maschinellen Lernen und der Verarbeitung natürlicher Sprache erkundet.
Wir haben gesehen, wie eine Implementierung mit scikit-learn aussehen kann, und die praktischen Anwendungen und Vorteile von Support Vector Machines beleuchtet.
Dieser Artikel stellt nur eine Einführung dar, die empfohlenen Ressourcen erlauben eine weitergehende Vertiefung. Aufgrund ihrer Vielseitigkeit und Effizienz ist es ratsam, SVMs zu verstehen, um sich als Datenwissenschaftler und ML-Ingenieur weiterzuentwickeln.
Als Nächstes können Sie sich die besten Modelle für maschinelles Lernen ansehen.