So prüfen Sie, ob eine Zahl in Python eine Primzahl ist

Inhaltsverzeichnis

In dieser Anleitung erfahren Sie, wie Sie mit Python ein Programm entwickeln, das ermittelt, ob eine bestimmte Zahl eine Primzahl ist oder nicht.

Wenn Sie sich bereits mit Programmieraufgaben beschäftigt haben, sind Sie möglicherweise auf die mathematische Fragestellung gestoßen, eine Primzahl zu identifizieren oder zu überprüfen. In den folgenden Minuten werden Sie eine optimale Lösung für diese Fragestellung kennenlernen.

In diesem Tutorial werden Sie:

Die Grundlagen von Primzahlen auffrischen.
Python-Code schreiben, um zu prüfen, ob eine Zahl eine Primzahl ist.
Den Code optimieren, um einen Algorithmus mit einer Laufzeit von O(√n) zu erreichen.

Legen wir los, um all dies und mehr zu entdecken.

Was ist eine Primzahl?

Beginnen wir mit einer Wiederholung der Definition von Primzahlen.

In der Zahlentheorie wird eine natürliche Zahl n als Primzahl bezeichnet, wenn sie exakt zwei Teiler hat: 1 und die Zahl selbst (n). Zur Erinnerung an Ihre Schulmathematik: Eine Zahl i wird als Teiler der Zahl n bezeichnet, wenn n durch i ohne Rest teilbar ist. ✅

Die nachfolgende Tabelle zeigt einige Zahlen, alle ihre Teiler und ob es sich um Primzahlen handelt.

n	Teiler	Primzahl?
1	1	Nein
2	1, 2	Ja
3	1, 3	Ja
4	1, 2, 4	Nein
7	1, 7	Ja
15	1, 3, 5, 15	Nein

Aus der obigen Tabelle können wir folgende Schlüsse ziehen:

2 ist die kleinste Primzahl.
1 ist ein Teiler jeder Zahl.
Jede Zahl n ist ein Teiler von sich selbst.

1 und n sind also die trivialen Teiler für jede Zahl n. Eine Primzahl darf keine anderen Teiler als diese beiden haben.

Das heißt, wenn Sie von 2 bis n-1 gehen, sollten Sie keinen nicht-trivialen Teiler finden, der n ohne Rest teilt.

O(n)-Algorithmus zur Überprüfung, ob eine Zahl in Python eine Primzahl ist

In diesem Abschnitt werden wir den oben beschriebenen Ansatz in einer Python-Funktion formalisieren.

Sie können mit dem range()-Objekt in Python alle Zahlen von 2 bis n – 1 durchlaufen.

In Python gibt range(start, stop, step) ein Bereichsobjekt zurück. Sie können dann über das Range-Objekt iterieren, um eine Sequenz vom Start bis zum Stopp -1 in definierten Schritten zu erhalten.

Da wir die Menge der ganzen Zahlen von 2 bis n-1 benötigen, können wir range(2, n) angeben und in Verbindung mit der for-Schleife verwenden.

Folgendes soll erreicht werden:

Wenn Sie eine Zahl finden, die n ohne Rest teilt, können Sie sofort feststellen, dass die Zahl keine Primzahl ist.

Wenn Sie den gesamten Zahlenbereich von 2 bis n – 1 durchlaufen haben, ohne eine Zahl zu finden, die n ohne Rest teilt, dann ist die Zahl eine Primzahl.

Python-Funktion zur Primzahlprüfung

Mit dem oben genannten können wir die Funktion is_prime() wie folgt definieren.


def is_prime(n):
  for i in range(2,n):
    if (n%i) == 0:
      return False
  return True

Analysieren wir nun die obige Funktionsdefinition.

Die obige Funktion is_prime() nimmt eine positive Ganzzahl n als Argument entgegen.
Wenn Sie im angegebenen Bereich von (2, n-1) einen Teiler finden, gibt die Funktion False zurück, da die Zahl keine Primzahl ist.
Sie gibt True zurück, wenn Sie die gesamte Schleife durchlaufen, ohne einen Teiler zu finden.

Als Nächstes rufen wir die Funktion mit Argumenten auf und überprüfen, ob das Ergebnis korrekt ist.


is_prime(2)
# True

is_prime(8)
# False

is_prime(9)
# False

is_prime(11)
# True

Wie die obige Ausgabe zeigt, sind 2 und 11 Primzahlen (die Funktion gibt True zurück). Und 8 und 9 sind keine Primzahlen (die Funktion gibt False zurück).

So optimieren Sie die Python-Funktion is_prime()

Hier können wir eine kleine Optimierung vornehmen. Beachten Sie die Liste der Teiler in der folgenden Tabelle.

Zahl	Teiler
6	1, 2, 3, 6
10	1, 2, 5, 10
18	1, 2, 3, 6, 9, 18

Nun, wir können feststellen, dass der einzige Teiler von n, der größer als n/2 ist, n selbst ist.

Das bedeutet, dass Sie nicht bis n – 1 iterieren müssen. Sie können die Schleife stattdessen nur bis n/2 laufen lassen.

Wenn Sie bis n/2 keinen nicht-trivialen Teiler finden, werden Sie auch keinen darüber hinaus finden.

Ändern wir nun die Funktion is_prime(), um nach Teilern im Bereich (2, n/2) zu suchen.


def is_prime(n):
  for i in range(2,int(n/2)):
    if (n%i) == 0:
      return False
  return True

Lassen Sie uns nun die Ausgabe mit einigen Funktionsaufrufen überprüfen.


is_prime(9)
# False

is_prime(11)
# True

Auch wenn es so aussieht, als hätten wir optimiert, ist dieser Algorithmus hinsichtlich der Laufzeitkomplexität nicht effizienter als der vorherige. Beide haben tatsächlich eine Laufzeitkomplexität von O(n): proportional zum Wert von n oder linear in n.

Können wir das besser machen? Ja, das können wir!

▶️ Fahren Sie mit dem nächsten Abschnitt fort, um zu sehen, wie Sie die Zeitkomplexität für Primzahltests verbessern können.

O(√n)-Algorithmus zum Überprüfen auf Primzahlen in Python

Tatsächlich treten die Teiler einer Zahl paarweise auf.

Wenn a ein Teiler der Zahl n ist, dann gibt es auch einen Teiler b, so dass axb = n oder einfach ab = n.

Überprüfen wir dies anhand eines Beispiels.

Die folgende Tabelle zeigt die paarweise auftretenden Teiler der Zahl 18. Sie können dies auch für ein paar andere Zahlen überprüfen, wenn Sie möchten.

Beachten Sie auch, dass √18 ungefähr 4,24 ist.

Und bei den paarweise auftretenden Teilern (a, b) können Sie sehen, dass, wenn a kleiner als 4,24 ist, dann b größer als 4,24 ist – in diesem Beispiel (2, 18) und (3, 6).

Teiler von 18 in Paaren

Die folgende Abbildung zeigt die Teiler von 18, die auf der Zahlengeraden gezeichnet wurden.

Wenn die Zahl n zufällig eine perfekte Quadratzahl ist, haben Sie a = b = √n als einen der Teiler.

▶️ Sehen Sie sich die Teiler von 36 in der folgenden Tabelle an. Da 36 eine perfekte Quadratzahl ist, ist a = b = 6 einer der Teiler. Für alle anderen Teilerpaare (a, b) gilt a < 6 und b > 6.

Teiler von 36 in Paaren

Zusammenfassend können wir Folgendes feststellen:

Jede Zahl n kann als n = axb geschrieben werden
Wenn n eine perfekte Quadratzahl ist, dann ist a = b = √n.
Und wenn a < b, dann a < √n und b > √n.
Andernfalls, wenn a > b, dann a > √n und b < √n.

Anstatt alle ganzen Zahlen bis n/2 zu durchlaufen, können Sie sich also dafür entscheiden, nur bis √n zu iterieren. Dies ist viel effizienter als unser bisheriger Ansatz.

So ändern Sie is_prime() in einen O(√n)-Algorithmus

Lassen Sie uns die Funktion optimieren, um Primzahlen in Python zu finden.


import math
def is_prime(n):
  for i in range(2,int(math.sqrt(n))+1):
    if (n%i) == 0:
      return False
  return True

Analysieren wir nun die obige Funktionsdefinition:

Um die Quadratwurzel einer Zahl zu berechnen, importieren wir das eingebaute Mathematikmodul von Python und verwenden die Funktion math.sqrt().
Da n möglicherweise keine perfekte Quadratzahl ist, müssen wir sie in eine ganze Zahl umwandeln. Verwenden Sie int(var), um var in ein int umzuwandeln.
Um sicherzustellen, dass wir tatsächlich bis zu √n prüfen, addieren wir eins, da die Funktion range() standardmäßig den Endpunkt des Bereichs ausschließt.

Die folgende Codezelle überprüft, ob unsere Funktion is_prime() korrekt funktioniert.


is_prime(8)
# False

is_prime(15)
# False

is_prime(23)
# True

Lassen Sie uns im nächsten Abschnitt ein paar einfache Diagramme erstellen, um O(n) und O(√n) visuell zu verstehen.

O(n) und O(√n) visuell vergleichen

▶️ Führen Sie das folgende Code-Snippet in einer Jupyter-Notebook-Umgebung Ihrer Wahl aus.


import numpy as np
import seaborn as sns
import pandas as pd


n = 20

x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)

Das obige Snippet veranschaulicht, wie man die Kurven für n und √n für einen Wertebereich zeichnen kann.

Wir verwenden die NumPy-Funktion arange(), um ein Array von Zahlen zu erstellen.
Dann sammeln wir die Werte von n und √n bis einschließlich 20 in einem Pandas DataFrame.
Als Nächstes zeichnen wir mit der Lineplot-Funktion von Seaborn.

Aus dem unten stehenden Diagramm können wir sehen, dass √n deutlich kleiner ist als n.

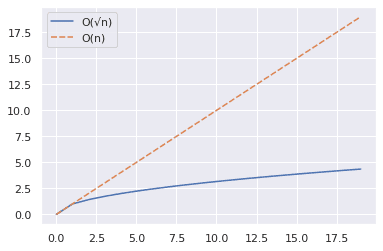
Erhöhen wir nun den Bereich auf 2000 und wiederholen die gleichen Schritte wie oben.


import numpy as np
import seaborn as sns
import pandas as pd


n = 2000

x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)

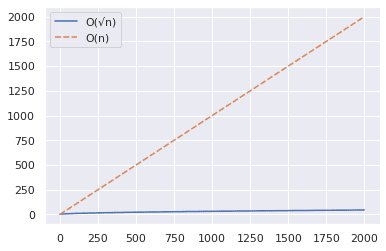
Aus dem obigen Diagramm können Sie schließen, dass der O(√n)-Algorithmus deutlich schneller ist, wenn Sie prüfen, ob eine große Zahl eine Primzahl ist.

Hier ist ein kurzes Beispiel: 2377 ist eine Primzahl – bestätigen Sie das! 😀

Während der O(n)-Ansatz etwa 2000 Schritte benötigt, kann der O(√n)-Algorithmus helfen, die Antwort in nur 49 Schritten zu finden. ✅

Fazit

⏳ Und nun ist es Zeit für eine kurze Zusammenfassung.

Um zu überprüfen, ob eine Zahl eine Primzahl ist, besteht der naive Ansatz darin, alle Zahlen im Bereich (2, n-1) zu durchlaufen. Wenn Sie keinen Teiler finden, der n teilt, dann ist n eine Primzahl.
Da der einzige Teiler von n, der größer als n/2 ist, n selbst ist, können Sie sich dafür entscheiden, nur bis n/2 zu laufen.
Beide oben genannten Ansätze haben eine Zeitkomplexität von O(n).
Da die Teiler einer Zahl paarweise auftreten, kann man nur bis √n iterieren. Dieser Algorithmus ist viel schneller als O(n). Der Vorteil ist erheblich, wenn man überprüft, ob eine große Zahl eine Primzahl ist oder nicht.

Ich hoffe, Sie verstehen nun, wie man in Python überprüft, ob eine Zahl eine Primzahl ist. Als Nächstes können Sie sich unser Tutorial zu Python-Programmen zu Zeichenkettenoperationen ansehen – in dem Sie lernen, wie man überprüft, ob Zeichenketten Palindrome, Anagramme und mehr sind.

Wir sehen uns in einem weiteren Tutorial. Bis dahin viel Spaß beim Programmieren! 👩🏽‍💻