So drucken Sie das Pascal-Dreieck in Python

Inhaltsverzeichnis

In diesem Leitfaden erfahren Sie, wie Sie das Pascal’sche Dreieck in Python für eine bestimmte Anzahl von Zeilen ausgeben können.

Zunächst werden wir uns mit dem Aufbau des Pascal’schen Dreiecks beschäftigen. Anschließend werden wir eine Python-Funktion schreiben und diese weiter optimieren.

▶️ Beginnen wir!

Was ist das Pascal’sche Dreieck und wie wird es aufgebaut?

Die Ausgabe des Pascal’schen Dreiecks für eine bestimmte Zeilenanzahl ist eine häufig gestellte Frage in Bewerbungsgesprächen.

Im Pascal’schen Dreieck mit n Zeilen enthält die Zeile Nummer i genau i Elemente.

Die erste Zeile hat also ein Element, nämlich die Zahl 1. Jedes Element in den folgenden Zeilen ergibt sich aus der Summe der beiden Zahlen direkt darüber.

Die folgende Grafik veranschaulicht den Aufbau des Pascal’schen Dreiecks für fünf Zeilen.

Pascal’sches Dreieck für numRows = 5 (Bild vom Autor)

Beachten Sie, dass Sie Nullen einfügen können, wenn sich über einer Zahl nur eine Zahl befindet.

📝 Als kurze Übung können Sie versuchen, das Pascal’sche Dreieck für n = 6 und n = 7 auf dieselbe Weise zu erstellen.

Nun wollen wir mit dem Schreiben von Code fortfahren. Sie können die Codeabschnitte direkt in Ihrem Browser in der Python-IDE von wdzwdz ausführen, während Sie das Tutorial durchgehen.

Python-Funktion zur Ausgabe des Pascal’schen Dreiecks

In diesem Abschnitt entwickeln wir eine Python-Funktion zur Ausgabe des Pascal’schen Dreiecks für eine beliebige Anzahl von Zeilen.

Dabei sind zwei Kernfragen zu berücksichtigen:

Wie werden die Einträge im Pascal’schen Dreieck mathematisch ausgedrückt?
Wie wird das Pascal’sche Dreieck mit der richtigen Formatierung und den passenden Abständen ausgegeben?

Lassen Sie uns diese Fragen nun beantworten.

#1. Wie lautet der Ausdruck für jeden Eintrag im Pascal’schen Dreieck?

Die Einträge im Pascal’schen Dreieck können durch die Formel für nCr ermittelt werden. Vielleicht erinnern Sie sich aus der Schulmathematik, dass nCr die Anzahl der Möglichkeiten angibt, r Elemente aus einer Menge von n Elementen auszuwählen.

Die Formel für nCr ist wie folgt:

nCr-Formel (Bild vom Autor)

Lassen Sie uns nun die Einträge im Pascal’schen Dreieck mithilfe der nCr-Formel darstellen.

Pascal’sche Dreieckseinträge mit nCr (Bild vom Autor)

Nun haben wir eine Methode gefunden, um die Einträge in der Matrix darzustellen.

#2. Wie passen wir die Abstände beim Drucken des Musters an?

Im Pascal’schen Dreieck mit numRows enthält die Zeile #1 einen Eintrag, Zeile #2 zwei Einträge usw. Um das Muster als Dreieck auszugeben, benötigen wir in Zeile #i jeweils numRows – i Leerzeichen. Dazu können wir die Range-Funktion von Python in Kombination mit einer for-Schleife verwenden.

Da die Bereichsfunktion standardmäßig den Endpunkt ausschließt, ist es wichtig, + 1 hinzuzufügen, um die benötigte Anzahl an führenden Leerzeichen zu erhalten.

Nachdem Sie nun wissen, wie Sie Einträge darstellen und Abstände beim Ausgeben des Pascal’schen Dreiecks anpassen, wollen wir mit der Definition der Funktion pascal_tri fortfahren.

Analyse der Funktionsdefinition

Was soll die Funktion pascal_tri also bewirken?

Die Funktion pascal_tri soll die Anzahl der Zeilen (numRows) als Argument akzeptieren.
Sie soll das Pascal’sche Dreieck mit numRows ausgeben.

Zur Berechnung der Fakultät verwenden wir die Fakultätsfunktion aus dem integrierten Mathematikmodul von Python.

▶️ Führen Sie die folgende Codezelle aus, um die Fakultätsfunktion zu importieren und in Ihrem aktuellen Modul zu verwenden.

from math import factorial

Das folgende Code-Snippet enthält die Funktionsdefinition.

def pascal_tri(numRows):
  '''Gibt das Pascal’sche Dreieck mit der angegebenen Anzahl von Zeilen aus.'''
  for i in range(numRows):
    # Schleife zum Erzeugen der führenden Leerzeichen
    for j in range(numRows-i+1):
      print(end=" ")
    
    # Schleife zum Erzeugen der Elemente der Zeile i
    for j in range(i+1):
      # nCr = n!/((n-r)!*r!)
      print(factorial(i)//(factorial(j)*factorial(i-j)), end=" ")

    # Gibt jede Zeile in einer neuen Zeile aus
    print("n")

Die Funktion arbeitet wie folgt:

Die Funktion pascal_tri hat einen erforderlichen Parameter numRows: die Anzahl der Zeilen.
Es gibt insgesamt numRows Zeilen. Für jede Zeile i fügen wir vor dem ersten Eintrag in der Zeile numRows – i führende Leerzeichen hinzu.
Wir verwenden dann die nCr-Formel, um die einzelnen Einträge zu berechnen. Für Zeile i sind die Einträge iCj, wobei j = {0,1,2,..,i}.
Beachten Sie, dass wir // verwenden, was eine ganzzahlige Division durchführt, da wir möchten, dass die Einträge ganze Zahlen sind.
Nachdem alle Einträge einer Zeile berechnet wurden, geben wir die nächste Zeile in einer neuen Zeile aus.

🔗 Da wir einen Docstring hinzugefügt haben, können Sie die integrierte Hilfefunktion von Python oder das Attribut __doc__ verwenden, um auf den Docstring der Funktion zuzugreifen. Das folgende Code-Snippet zeigt, wie es geht.

help(pascal_tri)

# Ausgabe
Help on function pascal_tri in module __main__:

pascal_tri(numRows)
  Gibt das Pascal’sche Dreieck mit der angegebenen Anzahl von Zeilen aus.

pascal_tri.__doc__

# Ausgabe
Gibt das Pascal’sche Dreieck mit der angegebenen Anzahl von Zeilen aus.

Nun wollen wir die Funktion mit der Anzahl der Zeilen als Argument aufrufen.

pascal_tri(3)

# Ausgabe
     1
    1 1
   1 2 1

Die ersten 3 Zeilen des Pascal’schen Dreiecks werden wie erwartet ausgegeben.

Ausgabe des Pascal’schen Dreiecks mit Rekursion

Im vorherigen Abschnitt haben wir den mathematischen Ausdruck für jeden Eintrag im Pascal’schen Dreieck ermittelt. Die Beziehung zwischen den Einträgen zweier aufeinanderfolgender Zeilen haben wir jedoch nicht genutzt.

Tatsächlich haben wir die vorherige Zeile verwendet, um die Einträge der nachfolgenden Zeile zu berechnen. Können wir das nicht verwenden und eine rekursive Implementierung der Funktion pascal_tri entwickeln?

Ja, machen wir das!

Bei einer rekursiven Implementierung ruft sich eine Funktion wiederholt selbst auf, bis der Basisfall eintritt. Beim Aufbau des Pascal’schen Dreiecks beginnen wir mit der ersten Zeile, die einen Eintrag 1 enthält, und bauen dann die folgenden Zeilen auf.

Der Funktionsaufruf von pascal_tri(numRows) ruft also wiederum pascal_tri(numRows-1) auf usw., bis der Basisfall pascal_tri(1) erreicht ist.

Betrachten Sie das Beispiel, in dem Sie die ersten 3 Zeilen des Pascal’schen Dreiecks ausgeben müssen. Die folgende Grafik veranschaulicht, wie die rekursiven Aufrufe auf den Stack geschoben werden und wie die rekursiven Funktionsaufrufe die Zeilen des Pascal’schen Dreiecks zurückgeben.

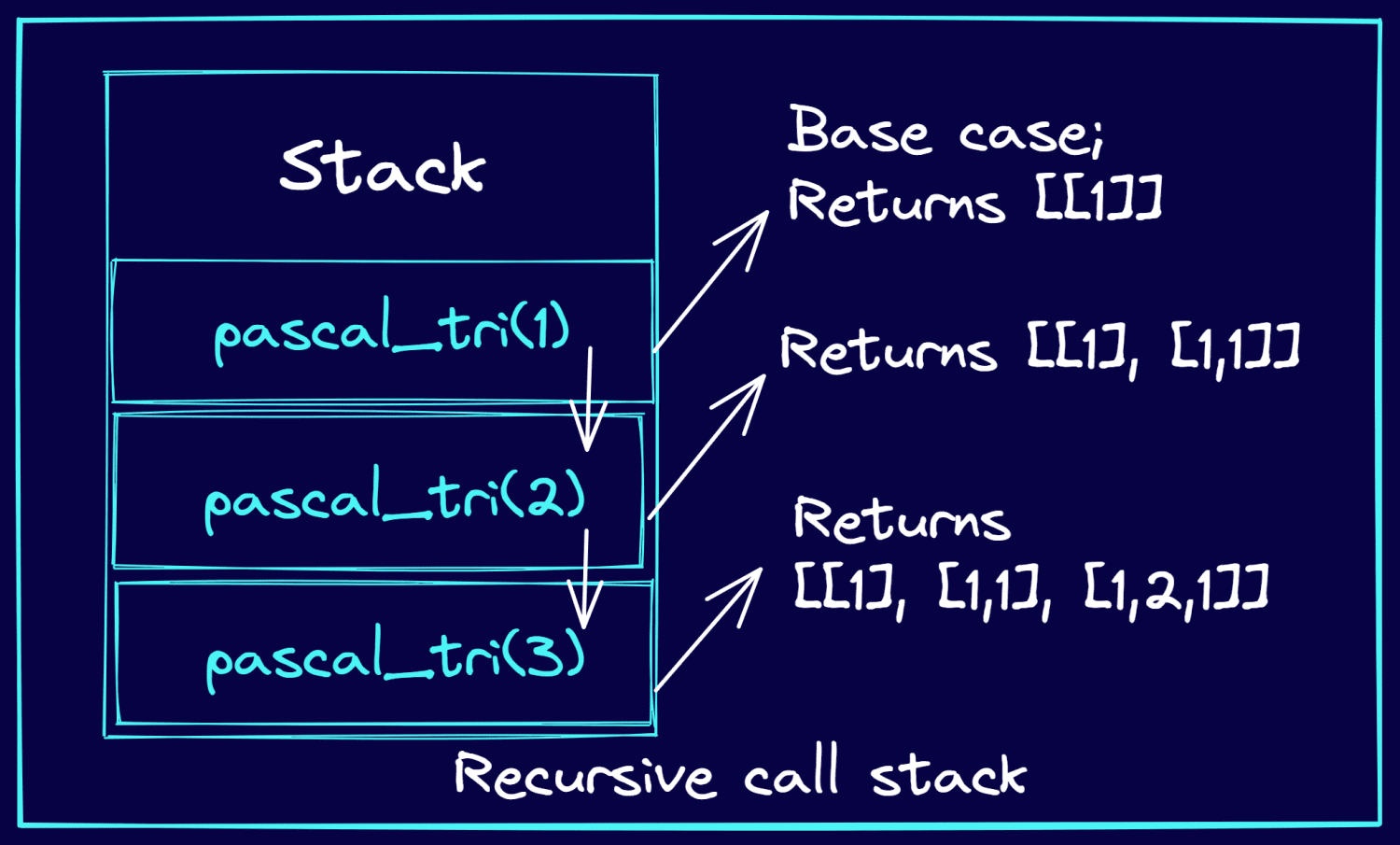Aufrufstack bei rekursiven Aufrufen (Bild vom Autor)

▶️ Führen Sie das folgende Code-Snippet aus, um die Zeilen des Pascal’schen Dreiecks rekursiv zu generieren.

def pascal_tri(numRows):
    '''Gibt das Pascal’sche Dreieck mit der angegebenen Anzahl von Zeilen aus.'''
    if numRows == 1:
        return [[1]] # Basisfall erreicht!
    else:
        res_arr = pascal_tri(numRows-1) # rekursiver Aufruf von pascal_tri
        # Verwendung der vorherigen Zeile zur Berechnung der aktuellen Zeile
        cur_row = [1] # Jede Zeile beginnt mit 1
        prev_row = res_arr[-1]
        for i in range(len(prev_row)-1):
            # Summe der zwei Einträge direkt darüber
            cur_row.append(prev_row[i] + prev_row[i+1])
        cur_row += [1] # Jede Zeile endet mit 1
        res_arr.append(cur_row)
        return res_arr

Hier sind einige Punkte, die es wert sind, beachtet zu werden:

Wir haben eine verschachtelte Liste als Datenstruktur verwendet, wobei jede Zeile im Pascal’schen Dreieck eine eigene Liste ist: [[Zeile 1], [Zeile 2],…,[Zeile n]].
Der Funktionsaufruf pascal_tri(numRows) löst eine Reihe rekursiver Aufrufe mit numRows – 1, numRows – 2 bis hin zu 1 als Argumente aus. Diese Aufrufe werden auf einen Stack geschoben.
Wenn numRows == 1 ist, haben wir den Basisfall erreicht und die Funktion gibt [[1]] zurück.
Nun wird die zurückgegebene Liste von den nachfolgenden Funktionen im Aufrufstack verwendet, um die nächste Zeile zu berechnen.
Wenn cur_row die aktuelle Zeile ist, ist cur_row[i] = vorherige_zeile[i] + vorherige_zeile[i+1] – die Summe der beiden Elemente direkt über dem aktuellen Index.

Da das zurückgegebene Array eine verschachtelte Liste (Liste von Listen) ist, müssen wir die Abstände anpassen und die Einträge ausgeben, wie in der Codezelle unten dargestellt.

tri_array = pascal_tri(5)

for i,row in enumerate(tri_array):
  for j in range(len(tri_array) - i + 1):
    print(end=" ") # führende Leerzeichen
  for j in row:
    print(j, end=" ") # Einträge ausgeben
  print("n")  # neue Zeile ausgeben

Die Ausgabe ist korrekt, wie unten zu sehen ist!

Python-Funktion zum Ausgeben des Pascal’schen Dreiecks für numRows ≤ 5

Beide gelernten Methoden funktionieren, um das Pascal’sche Dreieck für eine beliebige Anzahl von Zeilen numRows auszugeben.

Es gibt jedoch Fälle, in denen Sie das Pascal’sche Dreieck für eine kleinere Anzahl von Zeilen ausgeben möchten. Und wenn die Anzahl der Zeilen, die Sie ausgeben müssen, maximal 5 beträgt, können Sie eine einfache Methode anwenden.

Betrachten Sie die folgende Abbildung. Und beobachten Sie, wie die Potenzen von 11 mit den Einträgen im Pascal’schen Dreieck übereinstimmen. Beachten Sie auch, dass dies nur bis zur 4. Potenz von 11 funktioniert. Das heißt, 11 potenziert mit {0, 1, 2, 3, 4} ergibt die Einträge in den Zeilen 1 bis 5 des Pascal’schen Dreiecks.

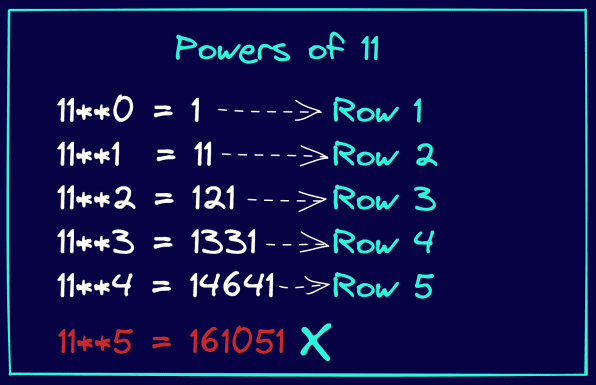
Lassen Sie uns die Funktionsdefinition wie unten gezeigt umschreiben:

def pascal_tri(numRows):
  '''Gibt das Pascal’sche Dreieck mit der angegebenen Anzahl von Zeilen aus.'''
  for i in range(numRows):
    print(' '*(numRows-i), end='')
    # Berechnet die Potenz von 11
    print(' '.join(str(11**i)))

So funktioniert die Funktion pascal_tri:

Wie bei den vorherigen Beispielen passen wir den Abstand an.
Dann verwenden wir Pythons Exponentiationsoperator (**), um die Potenzen von 11 zu berechnen.
Da die Potenzen von 11 standardmäßig ganze Zahlen sind, konvertieren wir sie mit str() in einen String. Jetzt haben wir die Potenzen von 11 als Strings.
Strings in Python sind iterierbar – wir können sie also durchlaufen und auf jeweils ein Zeichen zugreifen.
Als Nächstes können wir die Methode join() mit folgender Syntax verwenden: .join(), um Elemente in mit als Trennzeichen zu verbinden.
Hier benötigen wir ein einzelnes Leerzeichen zwischen den Zeichen, also ist ‚ ‚, und ist der String: Potenz von 11.

Lassen Sie uns überprüfen, ob die Funktion wie vorgesehen arbeitet.

pascal_tri(5)

# Ausgabe
     1
    1 1
   1 2 1
  1 3 3 1
 1 4 6 4 1

Als weiteres Beispiel rufen wir die Funktion pascal_tri mit 4 als Argument auf.

pascal_tri(4)

# Ausgabe
     1
    1 1
   1 2 1
  1 3 3 1

Ich hoffe, Sie verstehen nun, wie Sie das Pascal’sche Dreieck für numRows im Bereich von 1 bis 5 einfach ausgeben können.

Fazit

Folgendes haben wir gelernt:

Wie man das Pascal’sche Dreieck mit einer gegebenen Zeilenanzahl aufbaut: Jede Zahl in jeder Zeile ist die Summe der beiden Zahlen direkt darüber.
Eine Python-Funktion zu schreiben, die die Formel nCr = n!/(n-r)!.r! verwendet, um die Einträge des Pascal’schen Dreiecks zu berechnen.
Anschließend haben Sie eine rekursive Implementierung der Funktion kennengelernt.
Schließlich haben Sie die optimale Methode zum Aufbau des Pascal’schen Dreiecks für numRows bis zu 5 kennengelernt – die Verwendung der Potenzen von 11.

Wenn Sie Ihre Python-Kenntnisse verbessern möchten, lernen Sie, Matrizen zu multiplizieren, zu prüfen, ob eine Zahl eine Primzahl ist, und Probleme mit Stringoperationen zu lösen. Viel Spaß beim Programmieren!