Ez az oktatóanyag megtanítja Önnek, hogyan kell Python programot írni annak ellenőrzésére, hogy egy szám prímszámú-e vagy sem.
Ha valaha is részt vett kódolási teszteken, akkor találkozott a matematikai kérdéssel az elsődlegesség tesztjén vagy annak ellenőrzésére, hogy egy szám prím-e. A következő néhány percben pedig megtanulja, hogyan találja ki az optimális megoldást erre a kérdésre.
Ebben az oktatóanyagban a következőket teheti:
- áttekinteni a prímszámok alapjait,
- írjon Python kódot, hogy ellenőrizze, hogy egy szám prímszám-e, és
- optimalizálja tovább, hogy O(√n) futásidejű algoritmust kapjon.
Mindehhez és még sok máshoz kezdjük.
Tartalomjegyzék
Mi az a prímszám?
Kezdjük a prímszámok alapjainak áttekintésével.
A számelméletben egy n természetes számról azt mondják, hogy az prime ha pontosan két tényezője van: 1 és maga a szám (n). Emlékezzünk vissza az iskolai matematikából: az i számot az n szám tényezőjének mondjuk, ha i egyenlően osztja n-t. ✅
A következő táblázat felsorol néhány számot, azok összes tényezőjét, és azt, hogy prímszámúak-e.
nTényezők az elsődleges
A fenti táblázatból a következőket írhatjuk le:
- 2 a legkisebb prímszám.
- 1 minden szám tényezője.
- Minden n szám önmagában is tényező.
Tehát 1 és n triviális tényezők bármely n számra. Egy prímszámnak pedig e kettőn kívül nem lehet más tényezője.
Ez azt jelenti, hogy amikor 2-ről n – 1-re lép, nem találhat olyan nem triviális tényezőt, amely maradék nélkül osztja n-t.
O(n) Algoritmus annak ellenőrzésére, hogy egy szám Prime-e a Pythonban
Ebben a részben formalizáljuk a fenti megközelítést Python-függvénnyel.
A Pythonban a range() objektum segítségével 2-től n – 1-ig minden számot végigcsikorgathat.
A Pythonban a range(start, stop, step) egy tartományobjektumot ad vissza. Ezután ismételheti a tartomány objektumot, hogy lépésenkénti lépésekben kapjon egy sorozatot az elejétől egészen a -1 megállításáig.
Mivel szükségünk van a 2-től n-1-ig terjedő egész számokra, megadhatjuk a range(2, n)-t, és a for ciklussal együtt használhatjuk.
Íme, mit szeretnénk tenni:
- Ha talál egy számot, amely n-t egyenletesen osztja el, maradék nélkül, azonnal megállapíthatja, hogy a szám nem prím.
- Ha végigpörgette a számok teljes tartományát 2-től egészen n – 1-ig anélkül, hogy olyan számot talált volna, amely egyenletesen osztja n-t, akkor a szám prím.
Python függvény a prímszám ellenőrzéséhez
A fentiek felhasználásával a következőképpen definiálhatjuk az is_prime() függvényt.
def is_prime(n):
for i in range(2,n):
if (n%i) == 0:
return False
return True
Most elemezzük a fenti függvénydefiníciót.
- A fenti is_prime() függvény egy n pozitív egész számot vesz fel argumentumként.
- Ha talál egy tényezőt a megadott (2, n-1) tartományban, a függvény False értéket ad vissza – mivel a szám nem prímszám.
- És igazat ad vissza, ha a teljes hurkon bejárja anélkül, hogy tényezőt találna.
Ezután hívjuk meg a függvényt argumentumokkal, és ellenőrizzük, hogy a kimenet helyes-e.
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True
A fenti kimenetben azt látja, hogy 2 és 11 prím (a függvény True-t ad vissza). És 8 és 9 nem prímszám (a függvény False értéket ad vissza).
Az is_prime() Python függvény optimalizálása
Itt tehetünk egy kis optimalizálást. Vegye figyelembe a tényezők listáját az alábbi táblázatban.
Számtényezők 61, 2, 3, 6101, 2, 5, 10181, 2, 3, 6, 9, 18
Nos, láthatjuk, hogy n egyetlen tényezője, amely nagyobb n/2-nél, maga az n.
Tehát ez azt jelenti, hogy nem kell egészen n – 1-ig hurkolnia. Ehelyett csak n/2-ig futtathatja a ciklust.
Ha n/2-ig nem talál nem triviális tényezőt, akkor n/2-n túli tényezőt sem talál.
Most módosítsuk az is_prime() függvényt, hogy ellenőrizzük a (2, n/2) tartományban lévő tényezőket.
def is_prime(n):
for i in range(2,int(n/2)):
if (n%i) == 0:
return False
return True
Menjünk tovább, és ellenőrizzük a kimenetet néhány függvényhívással.
is_prime(9) # False is_prime(11) # True
Annak ellenére, hogy úgy tűnhet, hogy optimalizáltunk, ez az algoritmus nem hatékonyabb, mint az előző a futásidejű összetettség szempontjából. Valójában mindkettő O(n) futásidejű bonyolultságú: arányos n értékével vagy lineáris n-ben.
Tudunk jobban csinálni? Igen!
▶️ Lépjen a következő szakaszra, hogy meghatározza, hogyan javíthatja a prímszámok tesztelésének időbonyolítását.
O(√n) algoritmus a prímszám ellenőrzésére a Pythonban
Előfordul, hogy egy szám tényezői párban fordulnak elő.
Ha a az n szám tényezője, akkor létezik olyan b tényező is, amelyre axb = n, vagy egyszerűen ab = n.
Ellenőrizzük ezt egy példán keresztül.
Az alábbi táblázat a 18-as szám párokban előforduló tényezőit mutatja. Ha szeretné, ellenőrizheti ugyanezt néhány további számnál is.
Azt is vegye figyelembe, hogy a √18 körülbelül 4,24.
Az (a, b) párokban előforduló tényezőkből pedig látható, hogy ha a kisebb, mint 4,24, akkor b nagyobb, mint 4,24 – ebben a példában (2, 18) és (3, 6).
18-as faktorok párban
Az alábbi ábra a 18 tényezőit mutatja a számegyenesen ábrázolva.
Ha az n szám történetesen tökéletes négyzet, akkor a = b = √n lesz az egyik tényező.
▶️ Nézd meg a 36-os faktorokat az alábbi táblázatban. Mivel 36 tökéletes négyzet, a = b = 6 az egyik tényező. Az összes többi faktorpárra (a, b) a < 6 és b > 6 érvényes.
36-os faktorok párban
Összefoglalva a következőket kapjuk:
- Minden n szám felírható úgy, hogy n = axb
- Ha n tökéletes négyzet, akkor a = b = √n.
- És ha a < b, akkor a < √n és b > √n.
- Egyébként ha a > b, akkor a > √n és b < √n.
Tehát ahelyett, hogy n/2-ig végigpörgetné az összes egész számot, dönthet úgy, hogy √n-ig fut. És ez sokkal hatékonyabb, mint az előző megközelítésünk.
Hogyan módosítsuk az is_prime()-t O(√n) algoritmusra
Folytassa a függvény optimalizálásával, hogy ellenőrizze a prímszámokat a Pythonban.
import math
def is_prime(n):
for i in range(2,int(math.sqrt(n))+1):
if (n%i) == 0:
return False
return True
Most elemezzük a fenti függvénydefiníciót:
- Egy szám négyzetgyökének kiszámításához importáljuk a Python beépített matematikai modulját, és használjuk a math.sqrt() függvényt.
- Mivel lehet, hogy n nem tökéletes négyzet, egész számba kell öntnünk. Az int(var) használatával a var-t int-be öntheti.
- Annak érdekében, hogy megbizonyosodjunk arról, hogy valóban √n-ig ellenőrizzük, hozzáadunk egy plusz egyet, mivel a range() függvény alapértelmezés szerint kizárja a tartomány végpontját.
Az alábbi kódcella ellenőrzi, hogy az is_prime() függvényünk megfelelően működik-e.
is_prime(8) # False is_prime(15) # False is_prime(23) # True
A következő részben készítsünk néhány egyszerű grafikont az O(n) és O(√n) vizuális megértéséhez.
O(n) és O(√n) vizuális összehasonlítása
▶️ Futtassa a következő kódrészletet egy választott Jupyter notebook környezetben.
import numpy as np
import seaborn as sns
import pandas as pd
n = 20
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
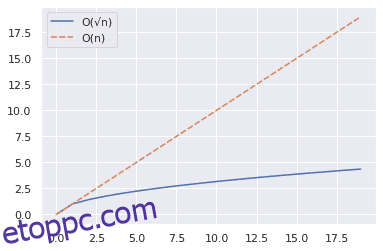
A fenti részlet megmutatja, hogyan ábrázolhatja az n és √n görbéit egy értéktartományhoz.
- A NumPy arange() függvényt használjuk számtömb létrehozására.
- Ezután összegyűjtjük n és √n értékét 20-ig, de nem számítva egy pandas DataFrame.
- Ezután ábrázoljuk a felhasználást seaborn vonalrajza() funkció.
Az alábbi ábrából láthatjuk, hogy √n lényegesen kisebb, mint n.
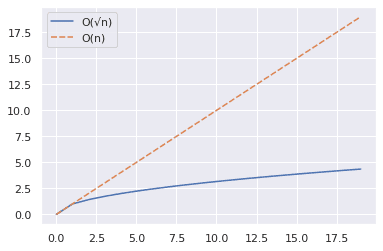
Most növeljük a tartományt 2000-re, és ismételjük meg a fenti lépéseket.
import numpy as np
import seaborn as sns
import pandas as pd
n = 2000
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
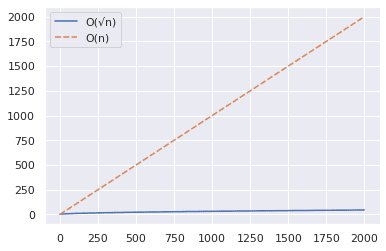
A fenti diagramból arra következtethet, hogy az O(√n) algoritmus lényegesen gyorsabb, ha azt teszteli, hogy nagy szám prímszámú-e.
Íme egy gyors példa: a 2377 egy prímszám – ellenőrizze ezt!😀
Míg az O(n) megközelítés 2000 lépésből áll, az O(√n) algoritmus mindössze 49 lépésben segíthet a válasz megtalálásában.✅
Következtetés
⏳ És itt az ideje egy gyors összefoglalónak.
- Annak ellenőrzésére, hogy egy szám prím-e, a naiv megközelítés az, hogy a (2, n-1) tartományban lévő összes számot végighurkoljuk. Ha nem talál n-t osztó tényezőt, akkor n prím.
- Mivel az n n/2-nél nagyobb tényezője csak maga az n, dönthet úgy, hogy csak n/2-ig fut.
- Mindkét fenti megközelítés időbonyolítása O(n).
- Mivel egy szám tényezői párban fordulnak elő, csak √n-ig futhat. Ez az algoritmus sokkal gyorsabb, mint az O(n). A nyereség pedig észrevehető annak ellenőrzésekor, hogy egy nagy szám prím-e vagy sem.
Remélem, megérti, hogyan ellenőrizheti, hogy egy szám prím-e a Pythonban. Következő lépésként tekintse meg a Python programokról szóló oktatóanyagunkat a karakterlánc-műveletekkel kapcsolatban – ahol megtanulhatja, hogyan ellenőrizheti, hogy a karakterláncok palindromok, anagrammák és egyebek-e.
Találkozunk egy másik oktatóanyagban. Addig is jó kódolást!👩🏽💻