A Big O Analysis az algoritmusok hatékonyságának elemzésére és rangsorolására szolgáló technika.
Ez lehetővé teszi a leghatékonyabb és leginkább méretezhető algoritmusok kiválasztását. Ez a cikk egy Big O Cheat Sheet, amely mindent elmagyaráz, amit a Big O jelölésről tudni kell.
Tartalomjegyzék
Mi az a Big O Analysis?
A Big O Analysis egy technika az algoritmusok skálázhatóságának elemzésére. Konkrétan azt kérdezzük, hogy mennyire hatékony egy algoritmus a bemeneti méret növekedésével.
A hatékonyság az, hogy a rendszer erőforrásait milyen jól használják fel a kimenet előállítása során. Azok az erőforrások, amelyekkel elsősorban foglalkozunk, az idő és a memória.
Ezért a Big O Analysis végrehajtása során a következő kérdéseket teszünk fel:
Az első kérdésre a válasz az algoritmus térbonyolultsága, míg a másodikra az időbonyolultsága. Mindkét kérdésre a Big O Notation nevű speciális jelölést használjuk. Erről legközelebb a Big O Cheat Sheet-ben lesz szó.
Előfeltételek
Mielőtt továbblépnék, el kell mondanom, hogy ahhoz, hogy a legtöbbet hozhassa ki ebből a Big O Cheat Sheetből, meg kell értenie egy kis algebrát. Ezen túlmenően, mivel Python-példákat fogok hozni, hasznos egy kicsit a Python megértése is. A mélyreható megértés szükségtelen, mivel nem fog kódot írni.
Hogyan végezzünk nagy O-elemzést
Ebben a részben bemutatjuk, hogyan kell elvégezni a Big O-elemzést.
A Big O komplexitáselemzés végrehajtásakor fontos megjegyezni, hogy az algoritmus teljesítménye a bemeneti adatok szerkezetétől függ.
Például a rendezési algoritmusok akkor futnak a leggyorsabban, ha a listában szereplő adatok már a megfelelő sorrendben vannak rendezve. Ez a legjobb forgatókönyv az algoritmus teljesítményéhez. Másrészt ugyanazok a rendezési algoritmusok a leglassabbak, ha az adatokat fordított sorrendben strukturálják. Ez a legrosszabb forgatókönyv.
A Big O Analysis végrehajtása során csak a legrosszabb forgatókönyvet vesszük figyelembe.
A tér összetettségének elemzése

Kezdjük ezt a Big O Cheat Sheet-et azzal, hogy bemutatjuk, hogyan kell elvégezni a tér összetettségének elemzését. Meg akarjuk vizsgálni, hogy az algoritmus kiegészítő memóriája hogyan skálázódik, amikor a bemenet egyre nagyobb és nagyobb lesz.
Például az alábbi függvény rekurziót használ az n-ről nullára történő hurokhoz. Térkomplexitása egyenesen arányos n-nel. Ennek az az oka, hogy ahogy n növekszik, úgy nő a függvényhívások száma a hívási veremben. Tehát a térkomplexitása O(n).
def loop_recursively(n):
if n == -1:
return
else:
print(n)
loop_recursively(n - 1)
Egy jobb megvalósítás azonban így nézne ki:
def loop_normally(n):
count = n
while count >= 0:
print(count)
count =- 1
A fenti algoritmusban csak egy további változót hozunk létre, és azt használjuk a ciklushoz. Ha n egyre nagyobbra nőne, akkor is csak egy további változót használnánk. Ezért az algoritmus állandó térkomplexitású, amit az „O(1)” szimbólum jelöl.
A fenti két algoritmus térkomplexitásának összehasonlításával arra a következtetésre jutottunk, hogy a while hurok hatékonyabb, mint a rekurzió. Ez a Big O Analysis fő célja: annak elemzése, hogyan változnak az algoritmusok, amikor nagyobb bemenettel futtatjuk őket.
Időkomplexitás-elemzés

Az időkomplexitás elemzésekor nem foglalkozunk az algoritmus által igénybe vett teljes idő növekedésével. Inkább a megtett számítási lépések növekedése aggaszt bennünket. Ennek az az oka, hogy a tényleges idő számos szisztémás és véletlenszerű tényezőtől függ, amelyeket nehéz megmagyarázni. Tehát csak a számítási lépések növekedését követjük nyomon, és feltételezzük, hogy minden lépés egyenlő.
Az időbonyolultság elemzésének bemutatásához vegye figyelembe a következő példát:
Tegyük fel, hogy van egy listánk a felhasználókról, ahol minden felhasználónak van azonosítója és neve. Feladatunk egy olyan függvény megvalósítása, amely azonosító megadása esetén visszaadja a felhasználó nevét. Íme, hogyan tehetjük ezt:
users = [
{'id': 0, 'name': 'Alice'},
{'id': 1, 'name': 'Bob'},
{'id': 2, 'name': 'Charlie'},
]
def get_username(id, users):
for user in users:
if user['id'] == id:
return user['name']
return 'User not found'
get_username(1, users)
A felhasználók listája alapján algoritmusunk végigfut a teljes felhasználói tömbön, hogy megtalálja a megfelelő azonosítóval rendelkező felhasználót. Ha 3 felhasználónk van, az algoritmus 3 iterációt hajt végre. Ha 10-ünk van, akkor 10-et teljesít.
Ezért a lépések száma lineárisan és egyenesen arányos a felhasználók számával. Tehát az algoritmusunk lineáris időbonyolultságú. Az algoritmusunkon azonban javíthatunk.
Tegyük fel, hogy a felhasználók listában való tárolása helyett egy szótárban tároljuk őket. Ekkor a felhasználó megkeresésére szolgáló algoritmusunk így néz ki:
users = {
'0': 'Alice',
'1': 'Bob',
'2': 'Charlie'
}
def get_username(id, users):
if id in users:
return users[id]
else:
return 'User not found'
get_username(1, users)
Tegyük fel, hogy ezzel az új algoritmussal 3 felhasználó szerepel a szótárunkban; több lépést is végrehajtunk a felhasználónév megszerzéséhez. És tegyük fel, hogy több felhasználónk van, mondjuk tíz. Ugyanannyi lépést hajtunk végre, mint korábban, hogy megszerezzük a felhasználót. A felhasználók számának növekedésével a felhasználónév megszerzéséhez szükséges lépések száma állandó marad.
Ezért ez az új algoritmus állandó bonyolultságú. Nem számít, hány felhasználónk van; a megtett számítási lépések száma ugyanannyi.
Mi az a Big O jelölés?
Az előző részben megvitattuk, hogyan lehet kiszámítani a Big O tér- és időbonyolultságát különböző algoritmusokhoz. A bonyolultságok leírására olyan szavakat használtunk, mint a lineáris és az állandó. A bonyolultságok leírásának másik módja a Big O jelölés használata.
A Big O jelölés egy algoritmus tér- vagy időbonyolultságának ábrázolásának módja. A jelölés viszonylag egyszerű; ez egy O, amelyet zárójel követ. A zárójelekbe n függvényét írjuk, amely az adott komplexitást reprezentálja.
A lineáris komplexitást n jelképezi, ezért O(n)-ként írnánk fel (az n-ből O-t). Az állandó komplexitást 1 jelenti, ezért O(1)-ként írnánk.
Vannak további bonyolultságok, amelyeket a következő részben tárgyalunk. Általában azonban egy algoritmus bonyolultságának megírásához kövesse a következő lépéseket:
Ennek eredménye az a kifejezés, amelyet zárójelünkben használunk.
Példa:
Tekintsük a következő Python-függvényt:
users = [
'Alice',
'Bob',
'Charlie'
]
def print_users(users):
number_of_users = len(users)
print("Total number of users:", number_of_users)
for i in number_of_users:
print(i, end=': ')
print(user)
Most kiszámítjuk az algoritmus Big O Time összetettségét.
Először felírjuk az nf(n) matematikai függvényét, amely reprezentálja az algoritmus által megtett számítási lépések számát. Emlékezzünk vissza, hogy n a bemeneti méretet jelöli.
A kódunkból a funkció két lépést hajt végre: az egyik a felhasználók számának kiszámításához, a másik a felhasználók számának kinyomtatásához. Ezután minden felhasználónál két lépést hajt végre: egyet az index és egyet a felhasználó kinyomtatására.
Ezért a megtett számítási lépések számát legjobban reprezentáló függvény f(n) = 2 + 2n alakban írható fel. Ahol n a felhasználók száma.
Továbblépve a második lépésre, kiválasztjuk a legdominánsabb kifejezést. A 2n egy lineáris tag, a 2 pedig egy állandó tag. A lineáris inkább domináns, mint konstans, ezért a 2n-t választjuk, a lineáris tagot.
Tehát a függvényünk most f(n) = 2n.
Az utolsó lépés az együtthatók kiküszöbölése. A mi függvényünkben 2 az együtthatónk. Tehát megszüntetjük. A függvény pedig f(n) = n lesz. Ezt a kifejezést használjuk a zárójelben.
Ezért az algoritmusunk időbonyolultsága O(n) vagy lineáris komplexitás.
Különböző Big O bonyolultságok
A Big O Cheat Sheet utolsó része bemutatja a különböző összetettségeket és a kapcsolódó grafikonokat.
#1. Állandó

Az állandó komplexitás azt jelenti, hogy az algoritmus állandó mennyiségű teret használ (a térkomplexitás elemzésekor) vagy állandó számú lépést (az időbonyolultság elemzésekor). Ez a legoptimálisabb komplexitás, mivel az algoritmusnak nincs szüksége további térre vagy időre, ahogy a bemenet növekszik. Ezért nagyon skálázható.
Az állandó komplexitást O(1)-ként ábrázoljuk. Nem mindig lehet azonban olyan algoritmusokat írni, amelyek állandó komplexitásban futnak.
#2. Logaritmikus
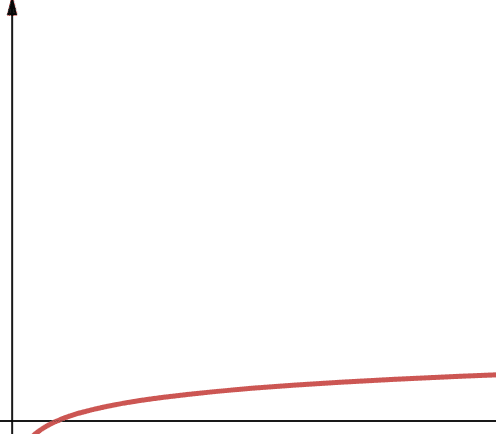
A logaritmikus komplexitást az O(log n) kifejezés jelöli. Fontos megjegyezni, hogy ha a logaritmusalap nincs megadva a Számítástechnikában, akkor feltételezzük, hogy 2.
Ezért a log n log2n. Ismeretes, hogy a logaritmikus függvények először gyorsan növekednek, majd lelassulnak. Ez azt jelenti, hogy skálázódnak és hatékonyan működnek egyre nagyobb számú n-nel.
#3. Lineáris
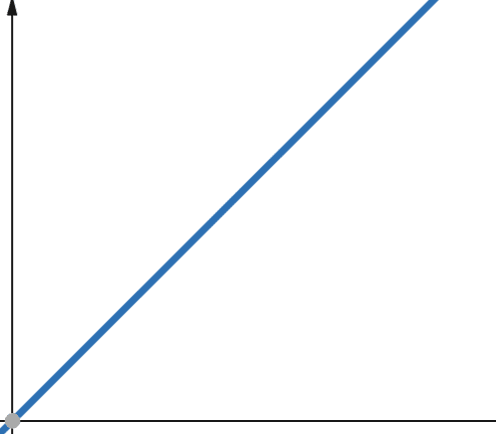
Lineáris függvényeknél, ha a független változó p tényezővel skálázódik. A függő változó p azonos tényezőjével skálázódik.
Ezért egy lineáris összetettségű függvény a bemeneti mérettel azonos tényezővel nő. Ha a bemeneti méret megduplázódik, akkor a számítási lépések száma vagy a memóriahasználat is megnő. A lineáris komplexitást az O(n) szimbólum jelöli.
#4. Linearitmikus
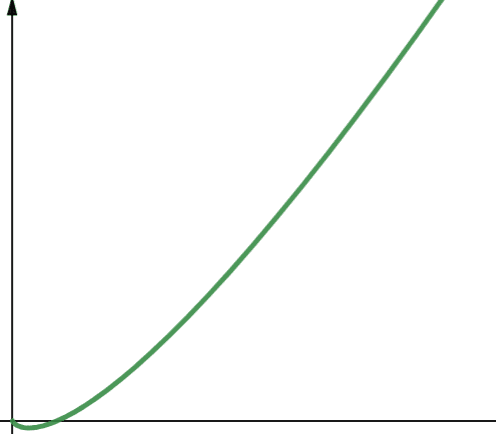
O (n * log n) linearitmikus függvényeket jelöl. A linearitmikus függvények lineáris függvények, szorozva a logaritmusfüggvénnyel. Ezért egy linearitmikus függvény valamivel nagyobb eredményeket ad, mint a lineáris függvények, ha log n nagyobb, mint 1. Ennek az az oka, hogy n növekszik, ha 1-nél nagyobb számmal megszorozzuk.
A log n 1-nél nagyobb minden 2-nél nagyobb n érték esetén (ne feledje, a log n log2n). Ezért minden 2-nél nagyobb n érték esetén a linearitmikus függvények kevésbé skálázhatók, mint a lineáris függvények. Ebből n a legtöbb esetben nagyobb, mint 2. Tehát a linearitmikus függvények általában kevésbé skálázhatók, mint a logaritmikus függvények.
#5. Négyzetes
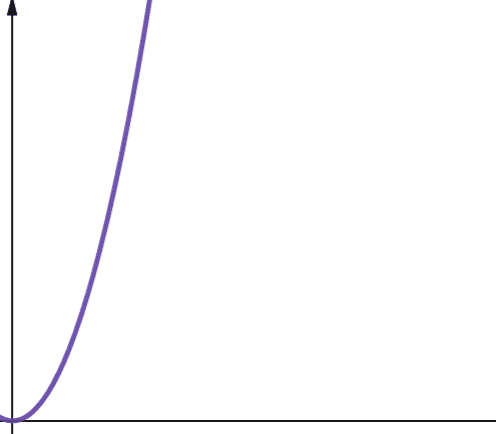
A kvadratikus komplexitást O(n2) jelenti. Ez azt jelenti, hogy ha a beviteli mérete 10-szeresére nő, a megtett lépések száma vagy a felhasznált terület 102-szeresére vagy 100-ra nő! Ez nem nagyon skálázható, és amint a grafikonon is látható, a bonyolultság nagyon gyorsan felpörög.
A négyzetes összetettség azokban az algoritmusokban jelentkezik, ahol n-szer hurkolunk, és minden iterációnál n-szer hurkolunk újra, például a Buborékos rendezésben. Bár általában nem ideális, időnként nincs más választása, mint másodfokú bonyolultságú algoritmusok megvalósítása.
#6. Polinom
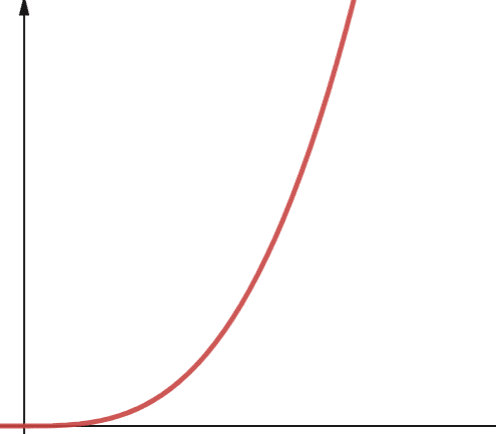
Egy polinomiális bonyolultságú algoritmust O(np) ábrázol, ahol p valamilyen állandó egész szám. P azt a sorrendet jelöli, amelyben n felemelkedik.
Ez a bonyolultság akkor merül fel, ha ap számú beágyazott hurokkal rendelkezik. A polinom komplexitása és a másodfokú komplexitás közötti különbség a kvadratikus 2 nagyságrendű, míg a polinomnak tetszőleges száma 2-nél nagyobb.
#7. Exponenciális
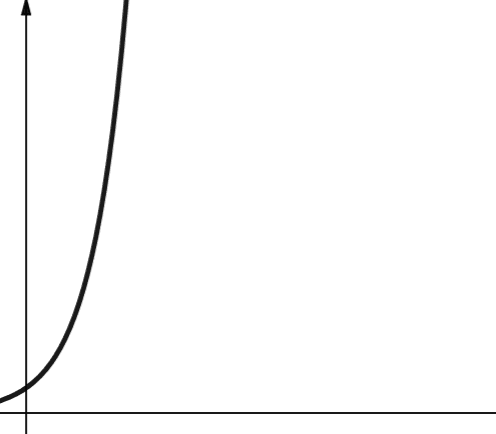
Az exponenciális komplexitás még gyorsabban nő, mint a polinomiális komplexitás. A matematikában az exponenciális függvény alapértelmezett értéke az e konstans (Euler-szám). A számítástechnikában azonban az exponenciális függvény alapértelmezett értéke 2.
Az exponenciális komplexitást az O(2n) szimbólum jelöli. Ha n értéke 0, 2n értéke 1. De ha n-t 5-re növeljük, 2n 32-re emelkedik. Az n eggyel történő növelése megduplázza az előző számot. Ezért az exponenciális függvények nem nagyon skálázhatók.
#8. Faktoriális
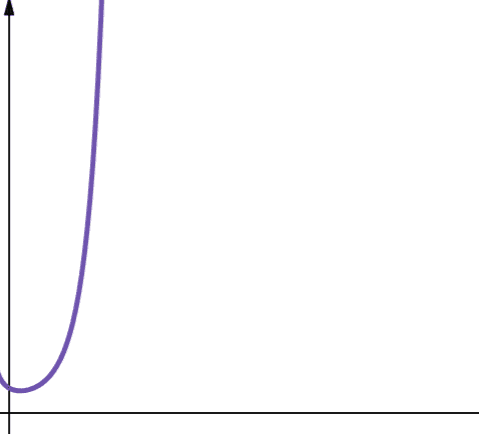
A faktorkomplexitást az O(n!) szimbólum jelöli. Ez a funkció is nagyon gyorsan növekszik, ezért nem méretezhető.
Következtetés
Ez a cikk a Big O-elemzéssel és annak kiszámításával foglalkozik. Megbeszéltük a különböző bonyolultságokat és azok méretezhetőségét is.
Ezután érdemes gyakorolni a Big O elemzést a Python rendezési algoritmuson.

