Die verschiedenen Mittelwertfunktionen sind ein wertvolles Werkzeug für vielfältige Aufgaben, ob es um die Auswertung von persönlichen Ausgaben, die Erfassung täglicher Routinen oder die Handhabung komplexer Datensätze geht. Diese Funktionen erlauben es, aus Daten wesentliche Erkenntnisse zu gewinnen und dadurch fundierte Entscheidungen zu treffen. In diesem Artikel wird detailliert auf die unterschiedlichen AVERAGE-Funktionen in Google Tabellen eingegangen, inklusive ihrer Anwendungsmöglichkeiten und praktischen Rechenbeispielen.
1 AVERAGE
Die Funktion AVERAGE ermittelt den arithmetischen Mittelwert einer Zahlenreihe, indem sie die Summe der Zahlen durch ihre Anzahl teilt. Die dazugehörige Syntax sieht wie folgt aus:
=AVERAGE(Bereich)
Hierbei steht ‚Bereich‘ für die Zellgruppe, deren Durchschnitt ermittelt werden soll.
Rechenbeispiel für AVERAGE
Nehmen wir an, es sollen die durchschnittlichen monatlichen Nebenkosten ermittelt werden, wobei sich die entsprechenden Daten in zwei Spalten befinden. Die Art der Nebenkosten wird in den Zellen A2:A5 der Spalte A aufgeführt, während die dazugehörigen Kosten in den Zellen B2:B5 der Spalte B stehen.
Um den mittleren monatlichen Betrag der Nebenkosten zu berechnen, lautet die Formel:
=AVERAGE(B2:B5)
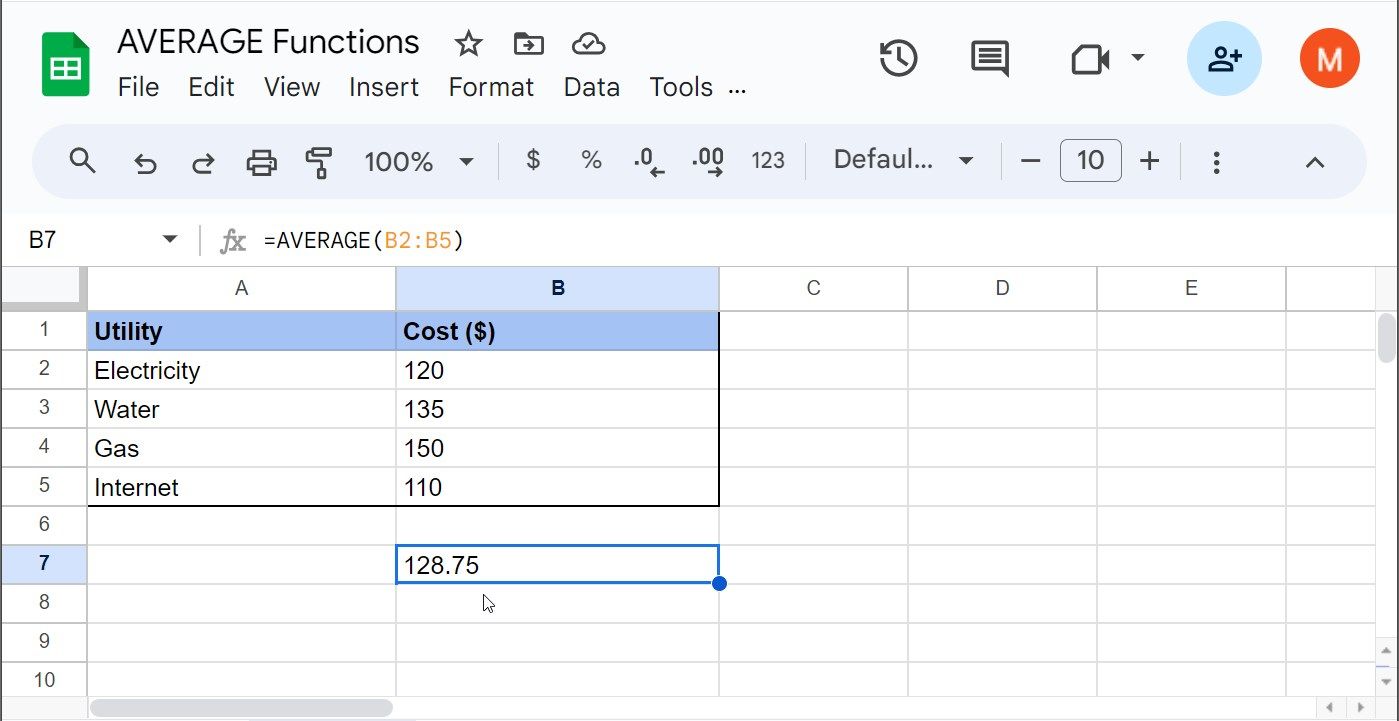
Im vorliegenden Beispiel betragen die durchschnittlichen monatlichen Nebenkosten 128,75 $.
2 AVERAGEA
Die AVERAGEA-Funktion kalkuliert den Durchschnitt eines Bereichs und berücksichtigt hierbei sowohl numerische Werte als auch Text. Text wird dabei als Nullwert behandelt. Diese Funktion erweist sich als nützlich, wenn der Durchschnitt eines Datensatzes ermittelt werden soll, der auch nicht-numerische Inhalte aufweist.
Die Syntax für die AVERAGEA-Funktion lautet:
=AVERAGEA(Bereich)
Dabei steht ‚Bereich‘ für die Zellen, die in die Durchschnittsberechnung einbezogen werden sollen.
Rechenbeispiel für AVERAGEA
Stellen wir uns vor, es wurden neue Methoden für das Aufgabenmanagement erlernt und daraufhin eine To-do-Liste erstellt. Bei der Erfassung der täglich erledigten Aufgaben wurden einige Aufgaben nicht als abgeschlossen markiert, sondern mit „N/A“ gekennzeichnet.
In diesem Szenario befinden sich die Anzahl der abgeschlossenen Aufgaben in den Zellen B2:B6. Um den Durchschnitt zu berechnen, wird folgende Formel verwendet:
=AVERAGEA(B2:B6)
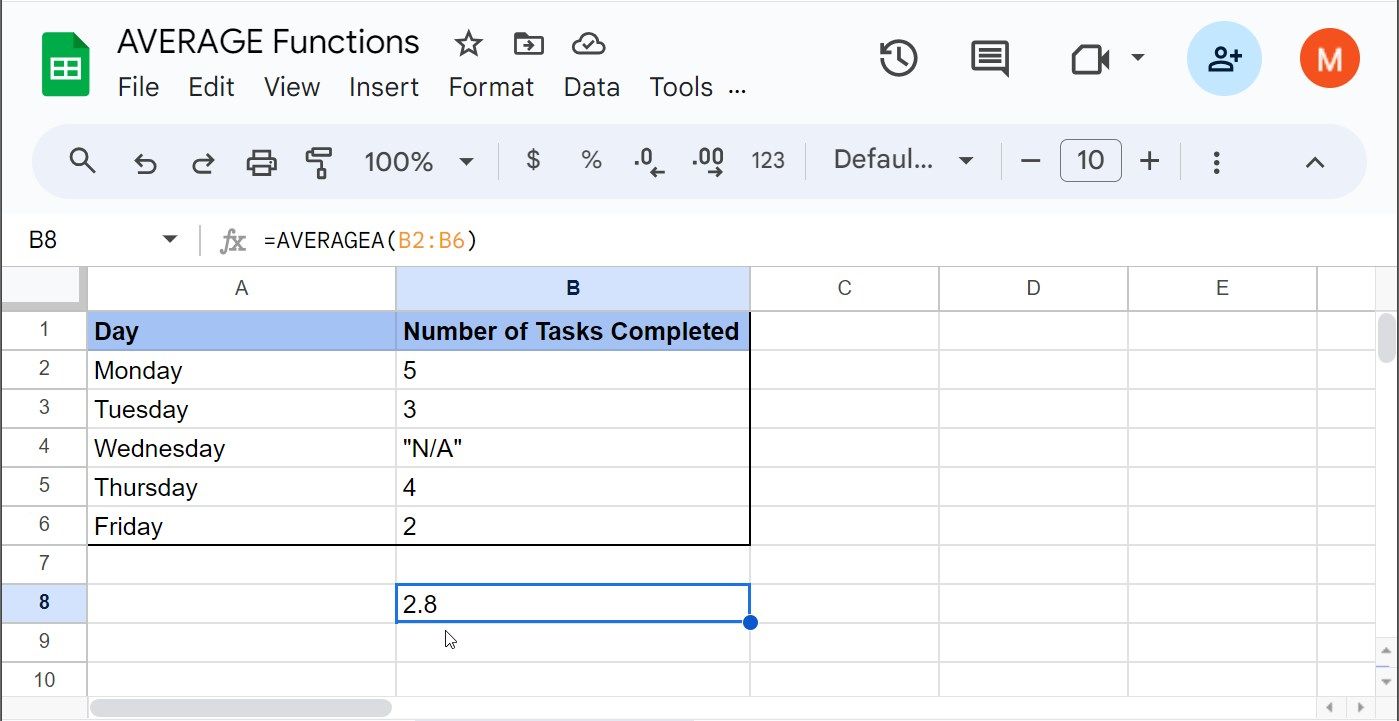
Da die Zelle B4 den Wert „N/A“ enthält, wird dieser bei der Berechnung als Null behandelt.
3 DAVERAGE
Die Funktion DAVERAGE berechnet den Mittelwert von Werten in einer bestimmten Spalte einer Datenbank, wobei nur die Zeilen berücksichtigt werden, welche die vorgegebenen Kriterien erfüllen. Die Syntax der Funktion DAVERAGE ist:
=DAVERAGE(Datenbank, Feld, Kriterien)
Hierbei steht ‚Datenbank‘ für den Zellbereich, der die Datenbank darstellt, ‚Feld‘ bezeichnet die Spalte, deren Durchschnitt berechnet werden soll und ‚Kriterien‘ ist der Bereich, der die Bedingungen enthält, welche die Auswahl der in den Durchschnitt einbezogenen Zeilen einschränken.
Rechenbeispiel für DAVERAGE
Angenommen, es soll die durchschnittliche Zeit erfasst werden, die mit dem Fernsehen verbracht wird, wobei nur die Tage berücksichtigt werden sollen, an denen mehr als 2 Stunden ferngesehen wurde. Die Tage, an denen ferngesehen wurde, sind in den Zellen A1:A5 aufgelistet und die dazugehörigen Fernsehstunden in den Zellen B2:B6.
Die Kriterien befinden sich in Spalte D. Da wir uns auf Tage mit mehr als 2 Stunden Fernsehen fokussieren, steht in Zelle D2 der Begriff ‚Stunden‘ und in Zelle D3 der Ausdruck ‚>2‘ (größer als 2).
Um die durchschnittliche tägliche Fernsehzeit in dieser Woche zu berechnen, wird die Formel verwendet:
=DAVERAGE(A1:B6; "Stunden"; D2:D3)
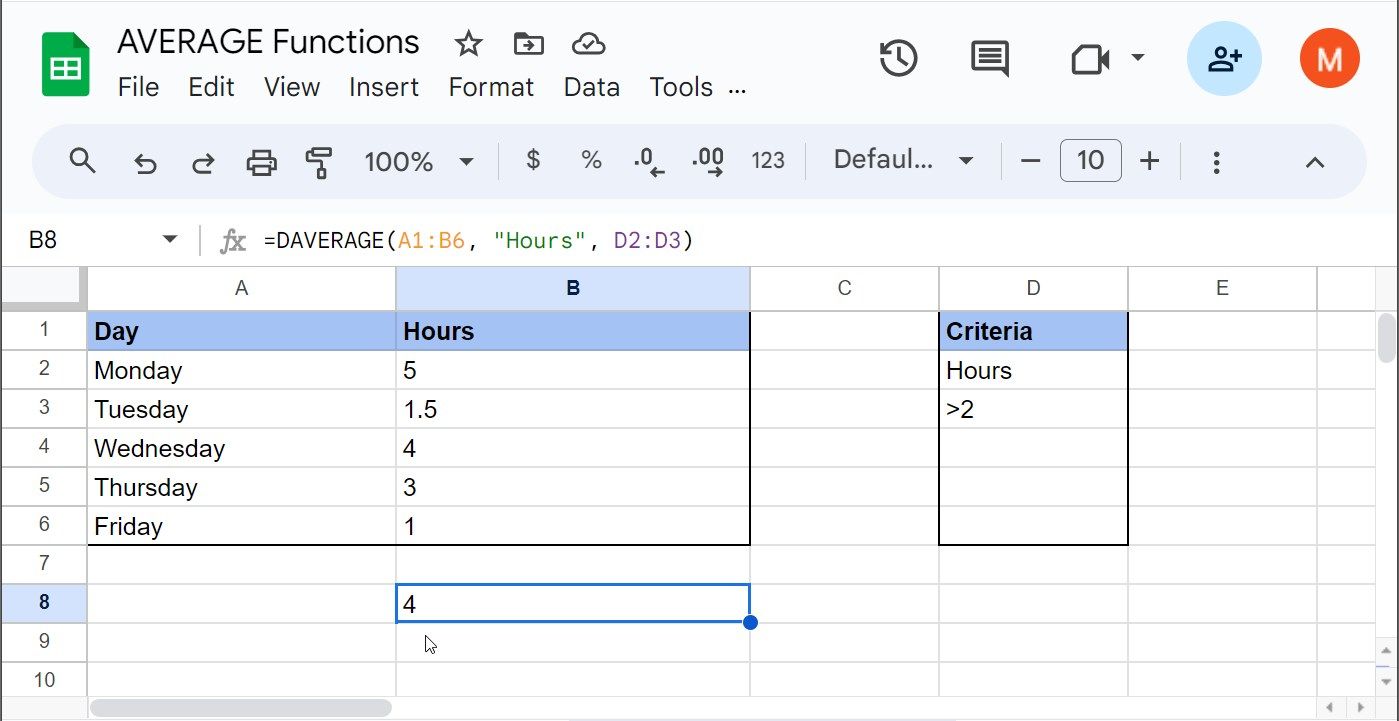
Im vorliegenden Fall wurde an drei Tagen der Woche mehr als 2 Stunden ferngesehen. Der Durchschnitt dieser Tage beläuft sich nun auf 4 Stunden.
4 AVERAGEIF
Die Funktion AVERAGEIF berechnet den Mittelwert von Zellen, die eine bestimmte Bedingung erfüllen. Die Syntax für die AVERAGEIF-Funktion lautet:
=AVERAGEIF(Bereich, Kriterien, [Mittelwert_Bereich])
Dabei steht ‚Bereich‘ für die Zellen, die auf die Kriterien hin überprüft werden sollen, ‚Kriterien‘ ist die Bedingung, welche bestimmt, welche Zellen in den Mittelwert einbezogen werden und ‚Mittelwert_Bereich‘ (optional) ist der tatsächliche Bereich der Zellen, dessen Mittelwert ermittelt werden soll.
Rechenbeispiel für AVERAGEIF
Angenommen, es soll der durchschnittliche wöchentliche Betrag für Kraftstoff ermittelt werden, jedoch nur für die Wochen, in denen mehr als 50 $ ausgegeben wurden. Die Ausgaben für Kraftstoff sind in den Zellen B2:B6 gelistet.
Um den Durchschnitt für die Werte über 50 $ zu bestimmen, wird folgende Formel verwendet:
=AVERAGEIF(B2:B6; ">50")

In diesem Beispiel beläuft sich der durchschnittliche Betrag für alle Ausgaben über 50 $ auf 65 $.
5 AVERAGEIFS
Die Funktion AVERAGEIFS ähnelt AVERAGEIF, ermöglicht jedoch die Anwendung mehrerer Kriterien. Die Syntax für die Funktion AVERAGEIFS lautet:
=AVERAGEIFS(Mittelwert_Bereich, Kriterien_Bereich1, Kriterium1, [Kriterien_Bereich2, Kriterium2], ...)
Hierbei steht ‚Mittelwert_Bereich‘ für den Zellbereich, dessen Mittelwert berechnet werden soll, ‚Kriterien_Bereich1‘ ist der Bereich, der auf das erste Kriterium hin überprüft wird, ‚Kriterium1‘ ist die erste Bedingung, die bestimmt, welche Zellen in den Durchschnitt einbezogen werden und es können weitere Bereiche und Kriterien spezifiziert werden.
Rechenbeispiel für AVERAGEIFS
Nehmen wir an, es werden Verkaufsdaten für verschiedene Produkte in unterschiedlichen Städten erfasst. Die Städte sind in den Zellen A2:A6 aufgeführt, die Produkte in den Zellen B2:B6, die Anzahl der verkauften Produkte in den Zellen C2:C6 und die Monate, in denen die Produkte verkauft wurden, in den Zellen D2:D6.
Es soll der durchschnittliche Absatz ermittelt werden, wobei die Stadt New York und das Produkt Gaming-PC berücksichtigt werden sollen. In diesem Fall lautet die Formel:
=AVERAGEIFS(C2:C6, A2:A6, "New York", B2:B6, "Gaming PC")
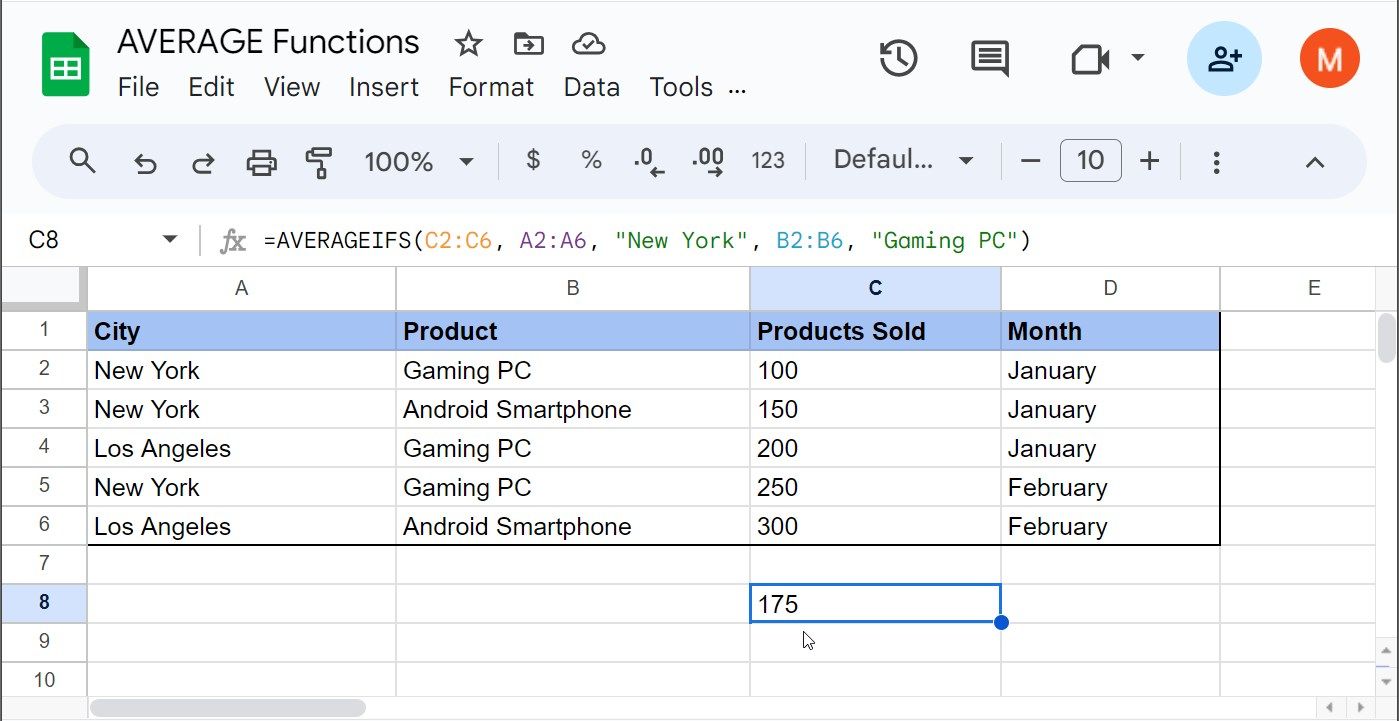
Dies liefert den durchschnittlichen Absatz von Gaming-PCs in New York über verschiedene Zeiträume hinweg. In diesem Beispiel liegt der Durchschnitt bei 175 verkauften Gaming-PCs in New York.
6 AVERAGE.WEIGHTED
Die Funktion AVERAGE.WEIGHTED berechnet einen gewichteten Durchschnitt, der besonders nützlich ist, wenn einige Werte in einem Datensatz stärker in die Mittelwertberechnung einfließen sollen als andere. Die Funktion berücksichtigt sowohl die Werte als auch deren jeweilige Gewichtung in der Berechnung. Ein gängiges Anwendungsbeispiel ist die Berechnung des Notendurchschnitts (GPA).
Die Syntax für die Funktion AVERAGE.WEIGHTED ist:
=AVERAGE.WEIGHTED(Werte, Gewichte)
Hierbei steht ‚Werte‘ für den Zellbereich, der die Werte für den Durchschnitt enthält und ‚Gewichte‘ steht für den Zellbereich, der die entsprechenden Gewichte für die Werte enthält.
Rechenbeispiel für AVERAGE.WEIGHTED
Angenommen, ein Student hat neue Lerntipps erhalten, um effektiver zu lernen und möchte nun einen gewichteten Durchschnitt der Lernstunden für verschiedene Fächer berechnen, wobei einige Fächer wichtiger sind als andere. Die Fächer stehen in den Zellen A2:A6, die Lernstunden in den Zellen B2:B6 und die Gewichte in den Zellen C2:C6.
Die Gewichtswerte reichen von 1 bis 4, wobei 1 „weniger wichtig“ und 4 „am wichtigsten“ bedeutet.
Um den gewichteten Durchschnitt der Lernstunden basierend auf der Bedeutung jedes Faches zu berechnen, wird folgende Formel verwendet:
=AVERAGE.WEIGHTED(B2:B6, C2:C6)
Diese Formel multipliziert die Lernstunden mit ihren entsprechenden Gewichten, summiert diese Werte und dividiert sie dann durch die Summe der Gewichte, um einen gewichteten Durchschnitt der Lernzeit zu erhalten.
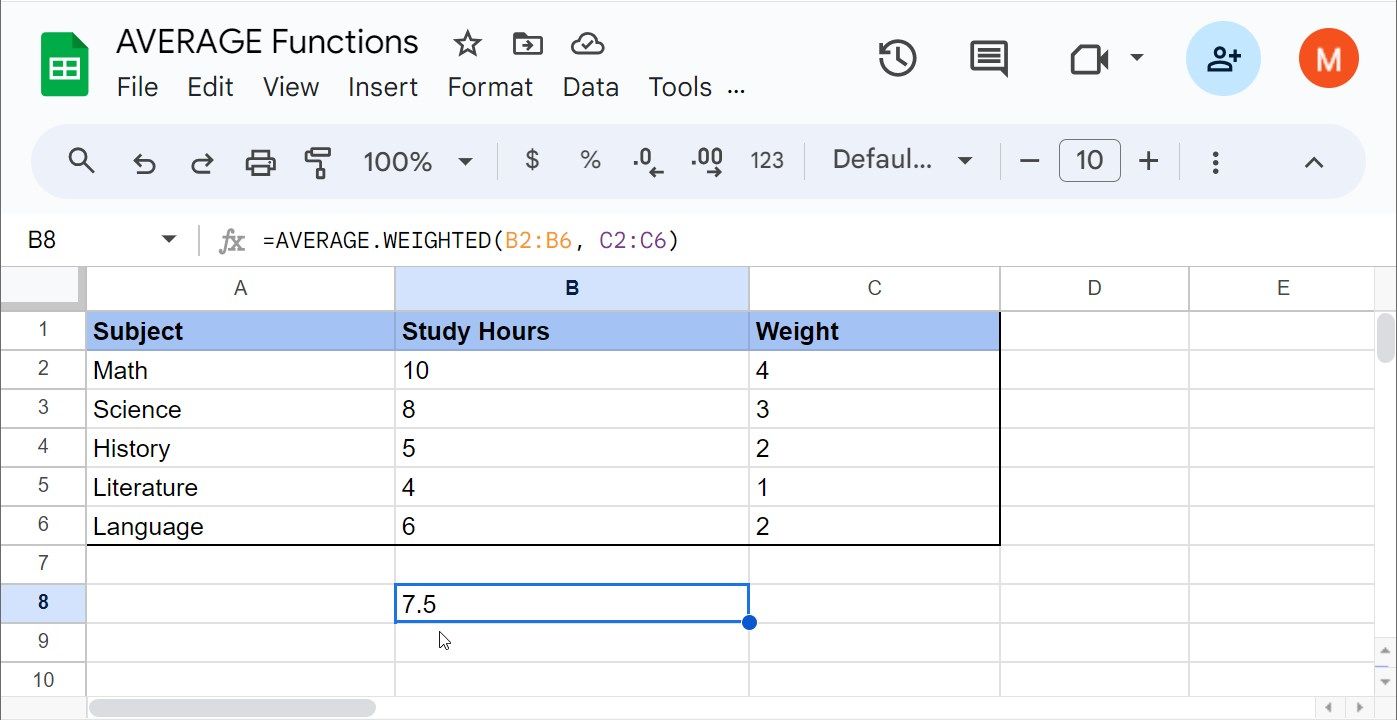
In diesem Fall beträgt die gewichtete durchschnittliche Lernzeit 7,5 Stunden. Dies bedeutet, dass die durchschnittliche Lernzeit 7,5 Stunden pro Fach beträgt, wenn die Bedeutung jedes Faches (Gewicht) berücksichtigt wird.
Folgendes zeigt, wie der gewichtete Durchschnitt bei der Bestimmung helfen kann, ob die aktuelle Lernzeit den akademischen Prioritäten entspricht:
- Mathematik: 10 Stunden (über dem Durchschnitt von 7,5 Stunden). Hier wird mehr Zeit als durchschnittlich investiert, was gut mit der Priorität/Gewichtung des Faches übereinstimmt.
- Naturwissenschaften: 8 Stunden (über 7,5 Stunden). Liegt leicht über dem gewichteten Durchschnitt und passt gut zur Gewichtung des Faches.
- Geschichte: 5 Stunden (unter 7,5 Stunden). Hier wird weniger Zeit als im Durchschnitt investiert, was aufgrund der geringeren Priorität/Gewichtung akzeptabel ist.
- Literatur: 4 Stunden (weit unter 7,5 Stunden). Die deutlich geringere Zeit entspricht der niedrigeren Priorität des Faches.
- Sprache: 6 Stunden (unter 7,5 Stunden). Hier wird etwas weniger Zeit investiert, liegt aber immer noch relativ nah am gewichteten Durchschnitt, was basierend auf der Gewichtung des Faches in Ordnung sein sollte.
Die AVERAGE-Funktionen bieten eine einfache und doch leistungsstarke Methode zur Datenverarbeitung. Durch die effiziente Nutzung dieser Funktionen können Datenanalysen in Google Tabellen problemlos durchgeführt und aussagekräftige Schlüsse aus komplexen Datensätzen gezogen werden.
Zusammenfassend lässt sich sagen, dass die AVERAGE-Funktionen eine vielseitige Hilfe für Datenanalysen darstellen. Mit ihrer Hilfe können präzise Mittelwerte berechnet und fundierte Entscheidungen auf Basis der vorliegenden Daten getroffen werden, egal ob im privaten oder geschäftlichen Bereich. Nutzen Sie die Möglichkeiten dieser Funktionen in Google Tabellen, um Ihre Datenanalysen zu optimieren und aussagekräftige Ergebnisse zu erzielen.